
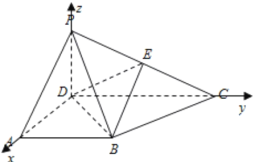
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据线面垂直的判定定理,即可证明结论成立;
(2)先由(1)得![]() 两两垂直,以
两两垂直,以![]() 点为坐标原点,以
点为坐标原点,以![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向,建立空间直角坐标系,分别求出平面
轴正方向,建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据向量夹角余弦值与二面角的大小,即可求出结果.
的一个法向量,根据向量夹角余弦值与二面角的大小,即可求出结果.
(1)因为侧面![]() 底面
底面![]() ,
,![]() ,
,
所以![]() 底面
底面![]() ,所以
,所以![]() ;
;
又底面![]() 是直角梯形,
是直角梯形,![]() ,
,
所以![]() ,
,
因此![]() ,所以
,所以![]() ;
;
又![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)由(1)可得![]() 两两垂直,
两两垂直,
因此以![]() 点为坐标原点,以
点为坐标原点,以![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向,建立如图所示的空间直角坐标系;
轴正方向,建立如图所示的空间直角坐标系;
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
由(1)可知![]() 平面
平面![]() ;所以
;所以![]() 为平面
为平面![]() 的一个法向量;
的一个法向量;
又因为![]() ,
,
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则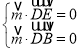 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
又二面角![]() 的大小为
的大小为![]() ,
,
所以![]() ,化简整理得
,化简整理得![]() ,
,
解得![]() ,
,
因为![]() 为侧棱
为侧棱![]() 上一点,所以
上一点,所以![]() ,
,
因此![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() .以极点为原点,极轴方向为
.以极点为原点,极轴方向为![]() 轴正半轴方向,利用相同单位长度建立平面直角坐标系,直线
轴正半轴方向,利用相同单位长度建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() 且
且![]() ).
).
(Ⅰ)写出圆![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①原命题为真,它的否命题为假;
②原命题为真,它的逆命题不一定为真;
③一个命题的逆命题为真,它的否命题一定为真;
④一个命题的逆否命题为真,它的否命题一定为真;
⑤“若![]() ,则
,则![]() 的解集为
的解集为![]() ”的逆命题.
”的逆命题.
其中真命题是___________.(把你认为正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() . 已知过点
. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值.若存在,求出点
为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com