
【题目】函数f(x)=x3﹣ax+1在区间(1,+∞)内是增函数,则实数a的取值范围是( )
A.a<3
B.a>3
C.a≤3
D.a≥3
科目:高中数学 来源: 题型:
【题目】
(1)已知点M(1,-3),N(1,2),P(5,y),且∠NMP=90°,则log8(7+y)=.
(2)若把本题中“∠NMP=90°”改为“log8(7+y)= ![]() ”,其他条件不变,则∠NMP=.
”,其他条件不变,则∠NMP=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 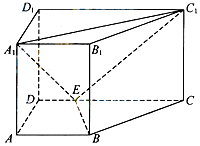
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: ①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 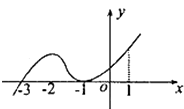
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木 ![]() 的高度
的高度 ![]() ,垂直放置的标杆
,垂直放置的标杆 ![]() 的高度
的高度 ![]() ,仰角
,仰角 ![]() 三点共线),试根据上述测量方案,回答如下问题:
三点共线),试根据上述测量方案,回答如下问题: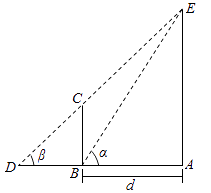
(1)若测得 ![]() ,试求
,试求 ![]() 的值;
的值;
(2)经过分析若干测得的数据后,大家一致认为适当调整标杆到树木的距离 ![]() (单位:)使
(单位:)使 ![]() 与
与 ![]() 之差较大时,可以提高测量的精确度.若树木的实际高为
之差较大时,可以提高测量的精确度.若树木的实际高为 ![]() ,试问
,试问 ![]() 为多少时,
为多少时, ![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的(产品净重,单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,下列命题中:①样本中净重大于或等于98克并且小于102克的产品的个数是60;②样本的众数是101;③样本的中位数是 ![]() ; ④样本的平均数是101.3.
; ④样本的平均数是101.3.
正确命题的代号是(写出所有正确命题的代号).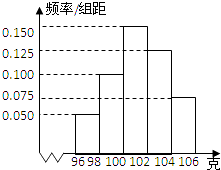
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com