
【题目】如图,四棱锥S﹣ABCD中,SD=CD=SC=2AB=2BC,平面ABCD⊥底面SDC,AB∥CD,∠ABC=90°,E是SD中点.
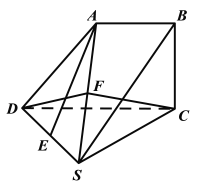
(1)证明:直线AE//平面SBC;
(2)点F为线段AS的中点,求二面角F﹣CD﹣S的大小.
【答案】(1)详见解析;(2)30°.
【解析】
(1)取SC中点G,连接BG,EG,推导出四边形AEGB为平行四边形,从而AE∥BG,进而AE∥平面SBC;
(2)取CD中点O,连接OS,OA ,推导出四边形ABCD为矩形,AO⊥CO,AO⊥CD,以O为原点,OS所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣CD﹣S的大小.
(1)证:如图,取SC中点G,连接BG,EG,
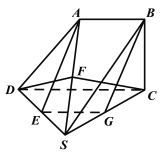
∵EG为△SDC的中位线,∴EG∥CD,且EG![]() ,
,
∵AB∥CD,且AB![]() ,∴EG∥CD,且EG=AB,
,∴EG∥CD,且EG=AB,
∴四边形AEGB为平行四边形,∴AE∥BG,
∵BG平面SBC,AE![]() 平面SBC,
平面SBC,
∴AE∥平面SBC;
(2)解:设AB=1,则BC=1,CD=2,取CD中点O,连接OS,OA ,
∴CO![]() ,
,
∵AB∥CD,∠ABC=90°,
∴四边形ABCO为矩形,∴AO⊥CO,AO⊥CD,
平面ABCD∩平面SDC=CD,∴AO⊥平面SDC,AO⊥SO,
∵△SDC为正三角形,∴SO⊥CD,
以O为原点,OS所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立如图所示的空间直角坐标系,
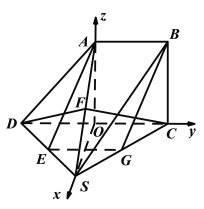
A(0,0,1),S(![]() ,0,0),C(0,1,0),D(0,﹣1,0),F(
,0,0),C(0,1,0),D(0,﹣1,0),F(![]() ,0,
,0,![]() ),
),
![]() (
(![]() ,1,
,1,![]() ),
),![]() (
(![]() ,﹣1,
,﹣1,![]() ),
),
设平面FCD的一个法向量![]() (a,b,c),
(a,b,c),
则 ,取x=1,得
,取x=1,得![]() (1,0,
(1,0,![]() ),
),
由题意取平面SDC的一个法向量![]() (0,0,1),
(0,0,1),
设二面角F﹣CD﹣S的大小为θ,
则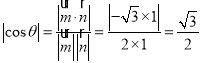 ,
,
由图可知,![]() 为锐角,∴θ=30°,
为锐角,∴θ=30°,
∴二面角F﹣CD﹣S的大小为30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
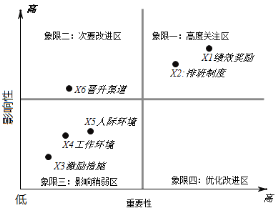
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在a>0,使得函数f(x)=6a2lnx+4ax与g(x)=x2﹣b在这两函数图象的公共点处的切线相同,则b的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某高校全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
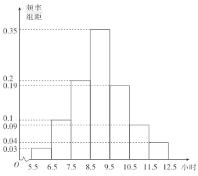
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com