
分析 由已知中函数f(x)满足的三个条件:①f(0)=0;②f(1-x)+f(x)=1x∈[0,1]; ③$x∈[0,\frac{1}{3}]$,$f(x)≥\frac{3}{2}x$恒成立.我们易得f($\frac{1}{2}$)=$\frac{1}{2}$,结合$x∈[0,\frac{1}{3}]$,$f(x)≥\frac{3}{2}x$成立,可得f($\frac{1}{3}$)≥$\frac{1}{2}$,又由f(x)为定义在[0,1]上的非减函数,可得当x∈[$\frac{1}{3}$,$\frac{1}{2}$]时,f(x)=$\frac{1}{2}$,进而得到答案.
解答 解:∵函数f(x)满足:f(1-x)+f(x)=1,x∈[0,1],则f($\frac{1}{2}$)=$\frac{1}{2}$,
且$x∈[0,\frac{1}{3}]$,$f(x)≥\frac{3}{2}x$,恒成立,则f($\frac{1}{3}$)≥$\frac{1}{2}$,
又∵函数f(x)为定义在[0,1]上的非减函数,
∴当x∈[$\frac{1}{3}$,$\frac{1}{2}$]时,f(x)=$\frac{1}{2}$,恒成立,
故f($\frac{3}{7}$)=$\frac{1}{2}$,f($\frac{4}{9}$)=$\frac{1}{2}$,则f($\frac{5}{9}$)=$\frac{1}{2}$,
则$f(\frac{3}{7})+f(\frac{5}{9})$=1
故答案为:1.
点评 本题考查的知识点是抽象函数及其应用,其中根据已知中,函数满足的条件,得到当x∈[$\frac{1}{3}$,$\frac{1}{2}$]时,f(x)=$\frac{1}{2}$恒成立,是解答本题的关键.本题主要考查了抽象函数及其应用,以及对新定义的理解,同时考查了计算能力和转化的思想,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
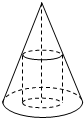 如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.
如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com