
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数,![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)列举可得总的基本事件和事件A中包含的基本事件,由古典概型可得;
(2)作出图象,由几何概型可得.
(1)由题意知本题是一个古典概型,设事件A为“方程有实根”,
总的基本事件共15个:(0,0)(0,1)(0,2)(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)(4,0)(4,1)(4,2),
其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含8个基本事件(a≥2b),(0,0)(1,0)(2,0)(2,1)(3,0)(3,1)(4,0)(4,1)(4,2),
∴事件A发生的概率为![]() ;
;
(2)由题意知本题是一个几何概型,
试验的全部结束所构成的区域为{(a,b)|0≤a≤4,0≤b≤2},
满足条件的构成事件A的区域为{(a,b)|0≤a≤4,0≤b≤2,a≥2b}.
∴所求的概率是![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方造一千多年,例如堑堵指底面为直角三角形,且测量垂直底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,如图,在堑堵![]() 中,
中,![]() ,若当阳马
,若当阳马![]() 的体积最大时,则堑堵
的体积最大时,则堑堵![]() 的体积为__________
的体积为__________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S3=9,a1 , a3 , a7成等比数列.
(1)求数列{an}的通项公式;
(2)若an≠a1时,数列{bn}满足bn=2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  ( t为参数).以原点为极点,x轴正半轴为极轴 建立极坐标系,圆C的方程为 ρ=2
( t为参数).以原点为极点,x轴正半轴为极轴 建立极坐标系,圆C的方程为 ρ=2 ![]() sinθ.
sinθ.
(1)写出直线l的普通方程和圆C的直角坐标方程;
(2)若点P的直角坐标为(1,0),圆C与直线l交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
,![]() …,
…,![]() 分成9组,制成了如图所示的频率分布直方图。
分成9组,制成了如图所示的频率分布直方图。

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使82%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由。
的值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
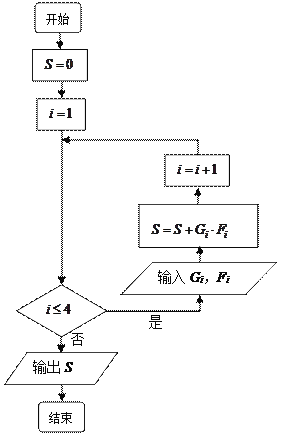
【题目】为了让学生更多的了解“数学史”知识,梁才学校高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组 | 组中值 | 频数 | 频率 |
(i) | (分数) | (Gi) | (人数) | (Fi) |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
(1)填充频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在
参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y= ![]() x2的焦点,离心率等于
x2的焦点,离心率等于 ![]() .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若 ![]() =λ1
=λ1 ![]() ,
, ![]() ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其焦点与双曲线
,其焦点与双曲线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点
的右顶点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
①设![]() ,当
,当![]() 为定值时,求
为定值时,求![]() 的值;
的值;
②设点![]() 是椭圆
是椭圆![]() 上的一点,满足
上的一点,满足![]() ,记
,记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com