
【题目】已知集合![]() ,若对于任意实数对
,若对于任意实数对![]() ,存在
,存在![]() ,使
,使![]() 成立,则称集合
成立,则称集合![]() 是“垂直对点集” .给出下列四个集合:
是“垂直对点集” .给出下列四个集合:
① ![]() ;
;
②![]() ;
;
③ ![]() ;
;
④![]() .
.
其中是“垂直对点集”的序号是( ).
A.①②③B.①②④C.①③④D.②③④
【答案】C
【解析】
由题意可得:集合![]() 是“垂直对点集”,即满足:曲线
是“垂直对点集”,即满足:曲线![]() 上过任意一点与原点的直线,都存在过另一点与原点的直线与之垂直,对①、②、③、④逐个分析即可.
上过任意一点与原点的直线,都存在过另一点与原点的直线与之垂直,对①、②、③、④逐个分析即可.
由题意知,若集合![]() 是“垂直对点集”,则对于任意
是“垂直对点集”,则对于任意![]() ,存在
,存在![]() ,使
,使![]() 成立,因此
成立,因此![]() ,
,
①![]() ,其图象向左向右和
,其图象向左向右和![]() 轴无限接近,向上和
轴无限接近,向上和![]() 轴无限接近,据幂函数的图象和性质可知,在图象上任取一点
轴无限接近,据幂函数的图象和性质可知,在图象上任取一点![]() ,连
,连![]() ,过原点作
,过原点作![]() 的垂线
的垂线![]() 必与
必与![]() 的图象相交,即一定存在点
的图象相交,即一定存在点![]() ,使得
,使得![]() 成立,故
成立,故![]() 是“垂直对点集”;
是“垂直对点集”;
②![]() ,(
,(![]() ),取
),取![]() ,则不存在点
,则不存在点![]() (
(![]() ),满足
),满足![]() ,因此
,因此![]() 不是“垂直对点集”;
不是“垂直对点集”;
③![]() ,其图象过点
,其图象过点![]() ,且向右向上无限延展,向左向下无限延展,据指数函数的图象和性质可知,在图象上任取一点A,连OA,过原点作
,且向右向上无限延展,向左向下无限延展,据指数函数的图象和性质可知,在图象上任取一点A,连OA,过原点作![]() 的垂线
的垂线![]() 必与
必与![]() 的图象相交,即一定存在点
的图象相交,即一定存在点![]() ,使得
,使得![]() 成立,故
成立,故![]() 是“垂直对点集”;
是“垂直对点集”;
④![]() ,在图象上任取一点
,在图象上任取一点![]() ,连
,连![]() ,过原点作直线
,过原点作直线![]() 的垂线
的垂线![]() ,因为
,因为![]() 的图象沿
的图象沿![]() 轴向左向右无限延展,且与
轴向左向右无限延展,且与![]() 轴相切,因此直线
轴相切,因此直线![]() 总会与
总会与![]() 的图象相交,故
的图象相交,故![]() 是“垂直对点集”,
是“垂直对点集”,
综上可得:只有①③④是“垂直对点集”.
故选:C


科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
)的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )

A. 向右平移![]() 个单位长度 B. 向左平移
个单位长度 B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度 D. 向左平移
个单位长度 D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了促进某产品的销售,随机调查了该产品的月销售单价x(单位:元/件)及相应月销量y(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下数表:
的数据进行了统计,得到如下数表:
月销售单价 | 8 | 8.5 | 9 | 9.5 | 10 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该公司年底开展促销活动,当月销售单价为7元/件时,其月销售量达到14.8万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过0.5万件,则认为所得到的回归直线方程是理想的,试问(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD,E,F分别为AB,CD的中点,将△ADE沿DE折起,使△ACD为等边三角形,如图所示,记二面角A-DE-C的大小为![]() .
.
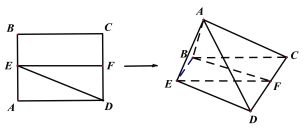
(1)证明:点A在平面BCDE内的射影G在直线EF上;
(2)求角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
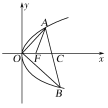
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,![]() (其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com