练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知过点A（﹣2，0）的直线与x=2相交于点C，过点B（2，0）的直线与x=﹣2相交于点D，若直线CD与圆x2+y2=4相切，则直线AC与BD的交点M的轨迹方程为 ．

    【答案】 +y2=1（x≠±2）
    【解析】解：设C（2，y1），D（﹣2，y2），则直线CD的方程为y﹣y1= （x﹣2），

    即（y1﹣y2）x﹣4y+2（y1+y2）=0，

    ∵直线CD与圆x2+y2=4相切，

    ∴ =2，整理得y1y2=4．

    设M（x0，y0），则直线AM的方程为y= （x+2），

    令x=2得y= ，即y1= ，

    同理得y2= ，

    ∵y1y2=4．

    ∴ =4，

    即x02+4y02=4，即 +y02=1．

    ∴M的轨迹方程为： =1（x≠±2）．

    所以答案是： =1（x≠±2）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x交于点B．

    （Ⅰ）求点P的坐标；
    （Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为 （0≤α＜π，t为参数），曲线C的极坐标方程为ρ= ．
    （Ⅰ）将曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
    （Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．
    （Ⅰ）求证：AC⊥平面BDEF；
    （Ⅱ）求直线DH与平面BDEF所成角的正弦值；
    （Ⅲ）求二面角H﹣BD﹣C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：

    x

    3

    4

    5

    6

    y

    25

    30

    40

    45

    由上表可得线性回归方程 = x+ ，据此模型预报广告费用为8万元时的销售额是（ ）
    附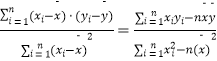： = ； = ﹣ x．
    A.59.5
    B.52.5
    C.56
    D.63.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣2x+1，g（x）=2aln（x﹣1）（a∈R）．
    （1）求函数h（x）=f（x）﹣g（x）的极值；
    （2）当a＞0时，若存在实数k，m使得不等式g（x）≤kx+m≤f（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的方程为（x﹣3）2+（y﹣4）2=16，过直线l：6x+8y﹣5a=0（a＞0）上的任意一点作圆的切线，若切线长的最小值为 ，则直线l在y轴上的截距为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】=在△ABC中，角A，B，C的对边分别为a，b，c，已知2（tanA+tanB）= + ．
    （Ⅰ）证明：a+b=2c；
    （Ⅱ）求cosC的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+（e﹣a）x﹣b，其中e为自然对数的底数．若不等式f（x）≤0恒成立，则 的最小值为 ．

    查看答案和解析>>

    同步练习册答案