
【题目】已知向量 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,k∈R.
,k∈R.
(1)当k为何值时,有 ![]() ∥
∥ ![]() ;
;
(2)若向量 ![]() 与
与 ![]() 的夹角为钝角,求实数k的取值范围.
的夹角为钝角,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占![]() ,女生中喜欢数学课程的占
,女生中喜欢数学课程的占![]() ,得到如下列联表.
,得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | |
男生 | |||
女生 | |||
合计 |
(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;
(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,求抽取的学生中至少有1名是女生的概率..
附:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1, ![]() ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)当a=1时,求f(x)在[1,4]上的最大值和最小值.
(2)若f (x)在( ![]() ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图(图1)及三视图(图2)如图所示,其中M,N分别是AF,BC的中点 
(1)求证:MN∥平面CDEF:
(2)求二面角A﹣CF﹣B的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
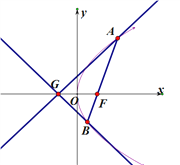
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com