
【题目】某战士在打靶中,连续射击两次,事件“至少有一次中靶”的对立事件是
A. 两次都不中 B. 至多有一次中靶
C. 两次都中靶 D. 只有一次中靶
科目:高中数学 来源: 题型:
【题目】命题“存在一个无理数,它的平方是有理数”的否定是
A. 任意一个有理数,它的平方是有理数 B. 任意一个无理数,它的平方不是有理数
C. 存在一个有理数,它的平方是有理数 D. 存在一个无理数,它的平方不是有理数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程分别是
的参数方程分别是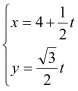 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极
轴的正半轴为极轴建立极
坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于点
交于点![]() (不同于原点),与直线
(不同于原点),与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
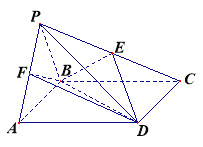
【题目】如图,四棱锥![]() 中,
中,![]() 是正三角形,四边形
是正三角形,四边形![]() 是矩形,且平面
是矩形,且平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() 时,求实数
时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)记函数![]() 的图象为曲线
的图象为曲线![]() .设点
.设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点.如果在曲线
上的不同两点.如果在曲线![]() 上存在点
上存在点![]() ,使得:①
,使得:①![]() ;②曲线
;②曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则称函数
,则称函数![]() 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数![]() 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,设圆
,设圆![]() 的半径为1,圆心在直线
的半径为1,圆心在直线![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:
①若命题p:x∈R,tan x=1;命题q:x∈R,x2-x+1>0,则命题“p∧﹁q”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是![]() =-3;
=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.
其中正确结论的序号为________(把你认为正确的结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com