
【题目】已知函数f(x)=ex﹣lnx+ax(a∈R).
(1)当a=﹣e+1时,求函数f(x)的单调区间;
(2)当a≥﹣1时,求证:f(x)>0.
【答案】(1)当x∈(0,1)时,f(x)单调递减;当x∈(1,+∞)时,f(x)单调递增(2)证明见解析
【解析】
(1)求导得到![]() ,根据导数的正负得到函数的单调区间.
,根据导数的正负得到函数的单调区间.
(2)求导得到![]() 判断h(x)在(0,+∞)上单调递增,
判断h(x)在(0,+∞)上单调递增,![]() ,使函数f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,代入计算得到证明.
,使函数f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,代入计算得到证明.
(1)f(x)=ex﹣lnx+(﹣e+1)x;令![]() ,得x=1;
,得x=1;
当x∈(0,1)时,f′(x)<0,f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增;
(2)证明:当a=﹣1时,f(x)=ex﹣lnx﹣x(x>0);
令![]() ,则
,则![]() ;
;
∴h(x)在(0,+∞)上单调递增;
又![]() ,h(1)=e﹣2>0;
,h(1)=e﹣2>0;
∴![]() ,使得
,使得![]() ,即
,即![]() ;
;
∴函数f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增;
∴函数f(x)的最小值为![]() ;
;
又函数![]() 是单调减函数;
是单调减函数;
∴f(x0)>1+1﹣ln1﹣1=1>0,即ex﹣lnx﹣x>0恒成立;
又ex>x>lnx;∴ex﹣lnx>0;又a≥﹣1,x>0;∴ax≥﹣x;
∴f(x)=ex﹣lnx+ax≥ex﹣lnx﹣x>0,得证.


科目:高中数学 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,如图(1),将其沿
,如图(1),将其沿![]() 折起使得平面
折起使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图(2).
,如图(2).
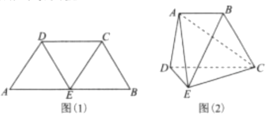
(1)证明:图(2)中的![]() 四点共面;
四点共面;
(2)求图(2)中平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求实数m的值;
(2)若α≥1,β≥1,f(α)+f(β)=4,求证:![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,点E在BC上,
,点E在BC上,![]() .
.
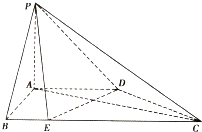
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若直线PE与平面PAC所成的角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
(1)求圆![]() 的普通方程及其极坐标方程;
的普通方程及其极坐标方程;
(2)设直线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() (异于极点),与直线
(异于极点),与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左.右顶点分别为A,B,离心率为
(a>b>0)的左.右顶点分别为A,B,离心率为![]() ,点P
,点P![]() 为椭圆上一点.
为椭圆上一点.
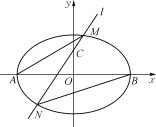
(1) 求椭圆C的标准方程;
(2) 如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为![]() ,
,![]() 为椭圆C的左右焦点,离心率为
为椭圆C的左右焦点,离心率为![]() ,短轴长为2。
,短轴长为2。
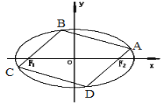
(1)求椭圆C的方程;
(2)如图,椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点![]() ,求该平行四边形ABCD面积的最大值.
,求该平行四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| <> | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com