
分析 (1)a=0时容易判断出f(x)是偶函数,对于a≠0时能够判断出是非奇非偶函数,只需举反例说明即可;
(2)求f′(x),则有f′(x)≥0在[2,+∞)上恒成立,便得到a≤2x3恒成立,从而得到a≤16,这便得出了a的取值范围.
解答 解:(1)当a=0时,f(x)=$\frac{1}{2}$x2,对任意x∈(-∞,0)∪(0,+∞),f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数;
当a≠0时,f(x)=$\frac{1}{2}$x2+$\frac{a}{x}$(a≠0,x≠0),取x=±1,得f(-1)+f(1)=1≠0,f(-1)-f(1)=-2a≠0,∴f(-1)≠-f(1),f(-1)≠f(1);
∴函数f(x)既不是奇函数,也不是偶函数;
(2)f′(x)=x-$\frac{a}{{x}^{2}}$=$\frac{{x}^{3}-a}{{x}^{2}}$;
∴x∈[1,+∞)时,$\frac{{x}^{3}-a}{{x}^{2}}$≥0恒成立,即a≤x3恒成立,x3在[1,+∞)的最小值为1,∴a≤1;
∴a的取值范围是(-∞,1].
点评 考查奇偶函数的定义,函数单调性和函数导数符号的关系,x3的单调性并根据单调性求最值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{n+2}{n}$ | B. | $\frac{2n+1}{2n-1}$ | C. | $-\frac{2n+1}{2n-1}$ | D. | -$\frac{n+1}{n-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
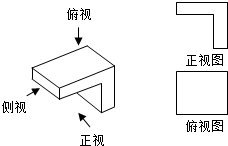 在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)
在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com