
| A. | [-5,5] | B. | [-$\sqrt{5}$,5] | C. | [-5,$\sqrt{5}$] | D. | [-$\sqrt{5},\sqrt{5}$] |
分析 如图所示,$|\overrightarrow{OM}|$=$\sqrt{{3}^{2}+{4}^{2}}$=5.$|\overrightarrow{ME}|$=1.由已知可得$\overrightarrow{ME}•\overrightarrow{MF}$=0,$\overrightarrow{OF}=\overrightarrow{OM}+\overrightarrow{MF}$,因此$\overrightarrow{ME}•\overrightarrow{OF}$=$\overrightarrow{ME}•\overrightarrow{OM}$=-5$cos<\overrightarrow{ME},\overrightarrow{MO}>$,由于$<\overrightarrow{ME},\overrightarrow{MO}>$∈[0,π],即可得出.
解答 解:如图所示,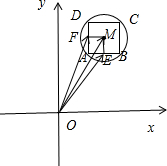
$|\overrightarrow{OM}|$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
$|\overrightarrow{ME}|$=1.
∵$\overrightarrow{ME}⊥\overrightarrow{MF}$,
∴$\overrightarrow{ME}•\overrightarrow{MF}$=0,
∵$\overrightarrow{OF}=\overrightarrow{OM}+\overrightarrow{MF}$,
∴$\overrightarrow{ME}•\overrightarrow{OF}$=$\overrightarrow{ME}$•$(\overrightarrow{OM}+\overrightarrow{MF})$
=$\overrightarrow{ME}•\overrightarrow{OM}$+$\overrightarrow{ME}•\overrightarrow{MF}$
=$\overrightarrow{ME}•\overrightarrow{OM}$
=-$|\overrightarrow{ME}||\overrightarrow{OM}|cos<\overrightarrow{ME},\overrightarrow{MO}>$
=-5$cos<\overrightarrow{ME},\overrightarrow{MO}>$,
∵$<\overrightarrow{ME},\overrightarrow{MO}>$∈[0,π],
∴$\overrightarrow{ME}•\overrightarrow{OF}$∈[-5,5].
故选:A.
点评 本题考查了数量积运算性质、圆的标准方程、向量三角形法则、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 37 | C. | 38 | D. | 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com