
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
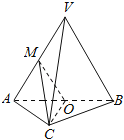
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
【答案】(1)证明解析;(2)证明见解析;(3)![]() .
.
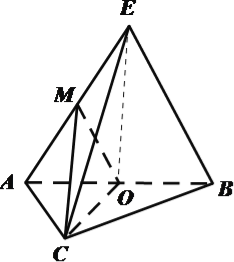
【解析】试题分析:(1)由中位线定理可得OM∥BE,故而EB∥平面MOC;
(2)由等腰三角形三线合一可得OC⊥AB,由平面EAB⊥平面ABC可得OC⊥平面EAB,故而平面MOC⊥平面EAB;
(3)连结OE,则OE为棱锥的高,利用等边三角形的性质求出OE,代入体积计算.
证明:(1)证明:∵O,M分别为AB,EA的中点,∴OM∥BE,
又∵EB平面MOC,OM平面MOC,
∴EB∥平面MOC.
(2)∵AC=BC,O 为AB中点,∴OC⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,
∴OC⊥平面EAB,又∵OC平面MOC,
∴平面MOC⊥平面 EAB.
(3)连结OE,则OE⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,OE平面EAB,
∴OE⊥平面ABC.
∵AC⊥BC,AC=BC=![]() ,∴AB=2,
,∴AB=2,
∵三角形EAB为等边三角形,∴OE=![]() .
.
∴三棱锥E﹣ABC的体积V=![]() EO=
EO=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
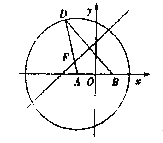
【题目】如图,在平面直角坐标系![]() 中,圆
中,圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,线段
上的动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设
,设![]() 分别为点
分别为点![]() 的横坐标,定义函数
的横坐标,定义函数![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 是偶函数;③
是偶函数;③![]() 在定义域上是增函数;
在定义域上是增函数;
④![]() 图象的两个端点关于圆心
图象的两个端点关于圆心![]() 对称;
对称;
⑤动点![]() 到两定点
到两定点![]() 的距离和是定值.
的距离和是定值.
其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
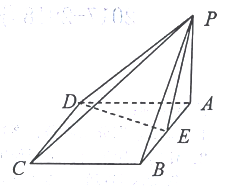
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足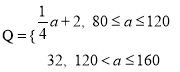 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com