
【题目】大城市往往人口密集,城市绿化在健康人民群众肺方面发挥着非常重要的作用,历史留给我们城市里的大山拥有品种繁多的绿色植物更是无价之宝.改革开放以来,有的地方领导片面追求政绩,对森林资源野蛮开发受到严肃查处事件时有发生.2019年的春节后,广西某市林业管理部门在“绿水青山就是金山银山”理论的不断指引下,积极从外地引进甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:

(1)据茎叶图求甲、乙两种树苗的平均高度;
(2)据茎叶图,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】双曲线![]() 的一条渐近线方程是
的一条渐近线方程是![]() ,坐标原点到直线AB的距离为
,坐标原点到直线AB的距离为![]() ,其中
,其中![]() ,
,![]() .
.
(1)求双曲线的方程;
(2)若![]() 是双曲线虚轴在y轴正半轴上的端点,过点B作直线交双曲线于点M,N,求
是双曲线虚轴在y轴正半轴上的端点,过点B作直线交双曲线于点M,N,求![]() 时,直线MN的方程.
时,直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个命题,其中正确命题的序号____________.
①![]() ;
;
②函数![]() 有
有![]() 个零点;
个零点;
③函数![]() 的图象关于点
的图象关于点![]() 对称。
对称。
④已知![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 的最小值是
的最小值是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() ∥平面
∥平面![]()
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角为300?如果存在,求出线段
所成的角为300?如果存在,求出线段![]() 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,
,![]() 是椭圆上任意一点,且点
是椭圆上任意一点,且点![]() 与两个焦点构成的三角形的面积的最大值为8.
与两个焦点构成的三角形的面积的最大值为8.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是上顶点,直线l交椭圆
是上顶点,直线l交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的重心恰好为点
的重心恰好为点![]() ,求直线l的方程的一般式.
,求直线l的方程的一般式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() .
.
(1)讨论f(x)的单调性,并证明f(x)有且仅有两个零点;
(2)设x0是f(x)的一个零点,证明曲线y=ln x 在点A(x0,ln x0)处的切线也是曲线![]() 的切线.
的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,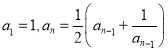 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com