
【题目】已知常数a>0,函数f(x)=ln(1+ax)﹣ ![]() .
.
(1)讨论f(x)在区间(0,+∞)上的单调性;
(2)若f(x)存在两个极值点x1 , x2 , 且f(x1)+f(x2)>0,求a的取值范围.
【答案】
(1)解:∵f(x)=ln(1+ax)﹣ ![]() .
.
∴f′(x)= ![]()
![]() =
= ![]() ,
,
∵(1+ax)(x+2)2>0,∴当1﹣a≤0时,即a≥1时,f′(x)≥0恒成立,则函数f(x)在(0,+∞)单调递增,
当0<a≤1时,由f′(x)=0得x=± ![]() ,则函数f(x)在(0,
,则函数f(x)在(0, ![]() )单调递减,在(
)单调递减,在( ![]() ,+∞)单调递增.
,+∞)单调递增.
(2)解:由(1)知,当a≥1时,f′(x)≥0,此时f(x)不存在极值点.
因此要使f(x)存在两个极值点x1,x2,则必有0<a<1,又f(x)的极值点值可能是x1= ![]() ,x2=﹣
,x2=﹣ ![]() ,
,
且由f(x)的定义域可知x>﹣ ![]() 且x≠﹣2,
且x≠﹣2,
∴﹣ ![]() >﹣
>﹣ ![]() 且﹣
且﹣ ![]() ≠﹣2,解得a≠
≠﹣2,解得a≠ ![]() ,则x1,x2分别为函数f(x)的极小值点和极大值点,
,则x1,x2分别为函数f(x)的极小值点和极大值点,
∴f(x1)+f(x2)=ln[1+ax1]﹣ ![]() +ln(1+ax2)﹣
+ln(1+ax2)﹣ ![]() =ln[1+a(x1+x2)+a2x1x2]﹣
=ln[1+a(x1+x2)+a2x1x2]﹣ ![]()
=ln(2a﹣1)2﹣ ![]() =ln(2a﹣1)2+
=ln(2a﹣1)2+ ![]() ﹣2.
﹣2.
令2a﹣1=x,由0<a<1且a≠ ![]() 得,
得,
当0<a< ![]() 时,﹣1<x<0;当
时,﹣1<x<0;当 ![]() <a<1时,0<x<1.
<a<1时,0<x<1.
令g(x)=lnx2+ ![]() ﹣2.
﹣2.
(i)当﹣1<x<0时,g(x)=2ln(﹣x)+ ![]() ﹣2,∴g′(x)=
﹣2,∴g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
故g(x)在(﹣1,0)上单调递减,g(x)<g(﹣1)=﹣4<0,
∴当0<a< ![]() 时,f(x1)+f(x2)<0;
时,f(x1)+f(x2)<0;
(ii)当0<x<1.g(x)=2lnx+ ![]() ﹣2,g′(x)=
﹣2,g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
故g(x)在(0,1)上单调递减,g(x)>g(1)=0,
∴当 ![]() <a<1时,f(x1)+f(x2)>0;
<a<1时,f(x1)+f(x2)>0;
综上所述,a的取值范围是( ![]() ,1).
,1).
【解析】(1)利用导数判断函数的单调性,注意对a分类讨论;(2)利用导数判断函数的极值,注意a的讨论及利用换元法转化为求函数最值问题解决.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e﹣x , 其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,试比较ea﹣1与ae﹣1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,AC∩BD=O, 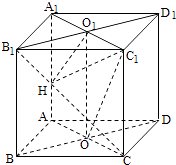 A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1﹣OB1﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,椭圆C1: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2:
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2: ![]() ﹣
﹣ ![]() =1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2=
=1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1. 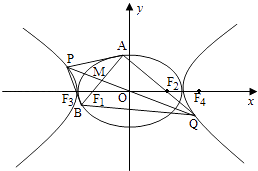
(1)求C1、C2的方程;
(2)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)= ![]() (|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
(|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,如果存在常数
上的函数,如果存在常数![]() ,对区间
,对区间![]() 的任意划分:
的任意划分:![]() ,和式
,和式![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 上的“绝对差有界函数”,注:
上的“绝对差有界函数”,注:![]() .
.
(1)求证:函数![]() 在
在![]() 上是“绝对差有界函数”;
上是“绝对差有界函数”;
(2)记集合![]() 存在常数
存在常数![]() ,对任意的
,对任意的![]() ,有
,有![]() 成立.
成立.
求证:集合![]() 中的任意函数
中的任意函数![]() 为“绝对差有界函数”;
为“绝对差有界函数”;
(3)求证:函数 不是
不是![]() 上的“绝对差有界函数”.
上的“绝对差有界函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|:|MN|=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com