
分析 根据函数奇偶性的定义建立方程关系求出a的值,结合充分条件和必要条件的定义进行判断即可.
解答 解:若f(x)=ln(ex+1)+ax为偶函数,
则f(-x)=f(x),
即ln(e-x+1)-ax=ln(ex+1)+ax,
即ln($\frac{1}{{e}^{x}}$+1)-ln(ex+1)=2ax,
即ln($\frac{1+{e}^{x}}{{e}^{x}}$)-ln(ex+1)=2ax,
即ln(ex+1)-lnex-ln(ex+1)=2ax,
即-x=2ax,
即2a=-1,则$a=-\frac{1}{2}$,
即$a=-\frac{1}{2}$是函数f(x)=ln(ex+1)+ax为偶函数的充要条件,
故答案为:充要.
点评 本题主要考查充分条件和必要条件的判断,根据函数奇偶性的定义建立方程关系求出a是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
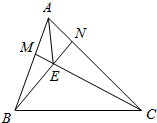 如图,在△ABC中,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AC}$,BN与CM交于点E,若$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=$\frac{5}{11}$.
如图,在△ABC中,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AC}$,BN与CM交于点E,若$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=$\frac{5}{11}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com