分析:(1)以点A为坐标原点O,以AB所成直线为Oy轴,以AA
1所在直线为Oz轴,以经过原点且与平面ABB
1A
1垂直的直线为Ox轴,建立空间直角坐标系,可求出A,B,A
1,C
1的坐标;
(2)取A
1B
1的中点M,易证AC
1与AM所成的角就是AC
1与侧面ABB
1A
1所成的角,求出
与
的坐标,利用向量的夹角公式求出此角即可.
解答: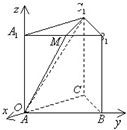
解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,
以AA
1所在直线为Oz轴,以经过原点且与平面ABB
1A
1垂直的直线为Ox轴,建立空间直角坐标系.
由已知得A(0,0,0),B(0,a,0),
A1(0,0,a),
C1(-a,,a).
②坐标系如上,取A
1B
1的中点M,于是有
M(0,,a),
连AM,MC
1有
=
(-a,0,0),
且
=(0,a,0),
=
(0,0,a),
由
•
=0,
•
=0,
所以,MC
1⊥面ABB
1A
1,
∴AC
1与AM所成的角就是AC
1与侧面ABB
1A
1所成的角.
∵
=
(-a,,a),
=
(0,,a),
∴
•
=
0++2a2=a2,
||=
=
a,
||=
=a,
∴
cos<,>=
=,
所以,
与
所成的角,即AC
1与侧面ABB
1A
1所成的角为30°.
点评:本题主要考查了直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

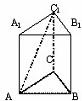 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为 解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,
解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.