
【题目】己知点![]() ,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.

(1)若直线OA的方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以直角坐标系的原点为极点,以
),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立坐标系,圆
轴的正半轴为极轴建立坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程(化为标准方程)及曲线
的直角坐标方程(化为标准方程)及曲线![]() 的普通方程;
的普通方程;
(2)若圆![]() 与曲线
与曲线![]() 的公共弦长为
的公共弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,给出下列命题:
,给出下列命题:
①若数列![]() 既是等差数列,又是等比数列,则数列
既是等差数列,又是等比数列,则数列![]() 是常数列.
是常数列.
②若等差数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
③若等比数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
④若各项为正数的等比数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
其中正确的命题个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD. 求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.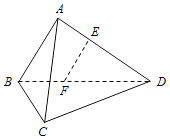
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(3)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com