
【题目】已知动圆经过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于点
交于点![]() ,
,![]() (
(![]() 为原点),求证:
为原点),求证:![]() 为线段
为线段![]() 中点.
中点.
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则
A. r2<r1<0 B. r2<0<r1 C. 0<r2<r1 D. r2=r1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求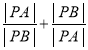 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家陈景润在哥德巴赫猜想的研究中取得了世界瞩目的成就,哥德巴赫猜想内容是“每个大于![]() 的偶数可以表示为两个素数的和”( 注:如果一个大于
的偶数可以表示为两个素数的和”( 注:如果一个大于![]() 的整数除了
的整数除了![]() 和自身外无其他正因数,则称这个整数为素数),在不超过
和自身外无其他正因数,则称这个整数为素数),在不超过![]() 的素数中,随机选取
的素数中,随机选取![]() 个不同的素数
个不同的素数![]() 、
、![]() ,则
,则![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量![]() 与冶炼时间
与冶炼时间![]() (从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(
加以说明(![]()
![]() ,则认为
,则认为![]() 与
与![]() 有较强的线性相关关系,否则认为没有较强的线性相关关系,
有较强的线性相关关系,否则认为没有较强的线性相关关系,![]() 精确到0.001);
精确到0.001);
(2)建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
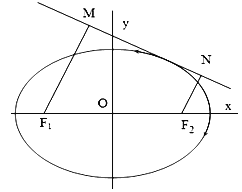
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上任意一点,且
上任意一点,且![]() 的最小值为0.
的最小值为0.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
,![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
,![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com