
【题目】设函数![]() ,则下列结论正确的是__________.(写出所有正确的编号)①
,则下列结论正确的是__________.(写出所有正确的编号)①![]() 的最小正周期为
的最小正周期为![]() ;②
;②![]() 在区间
在区间![]() 上单调递增;③
上单调递增;③![]() 取得最大值的
取得最大值的![]() 的集合为
的集合为![]() ④将
④将![]() 的图像向左平移
的图像向左平移![]() 个单位,得到一个奇函数的图像
个单位,得到一个奇函数的图像
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性;
的奇偶性;
(3)方程![]() 是否有实根?如果有实根
是否有实根?如果有实根![]() ,请求出一个长度为
,请求出一个长度为![]() 的区间
的区间![]() ,使
,使![]() ;如果没有,请说明理由(注:区间
;如果没有,请说明理由(注:区间![]() 的长度
的长度![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 件,需另投入成本
件,需另投入成本![]() ,当年产量不足80件时,
,当年产量不足80件时, ![]() (万元),当年产量不少于80件时
(万元),当年产量不少于80件时![]() (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为全等的等边三角形,
为全等的等边三角形, ![]() 分别为
分别为![]() 的中点.在此几何体中,下列结论中错误的为( )
的中点.在此几何体中,下列结论中错误的为( )

A. 直线![]() 与直线
与直线![]() 共面 B. 直线
共面 B. 直线![]() 与直线
与直线![]() 是异面直线
是异面直线
C. 平面![]() 平面
平面![]() D. 面
D. 面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的四边形ABCD,已知 ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)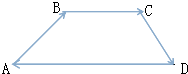
(1)若 ![]() 且﹣2≤x<1,求函数y=f(x)的值域;
且﹣2≤x<1,求函数y=f(x)的值域;
(2)若 ![]() 且
且 ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1.设集合P={1,2,3}和Q={﹣1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率
(1)已知关于x的二次函数f(x)=ax2﹣4bx+1.设集合P={1,2,3}和Q={﹣1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(2)在区间[1,5]和[2,4]上分别取一个数,记为a,b,求方程 ![]() +
+ ![]() =1表示焦点在x轴上且离心率小于
=1表示焦点在x轴上且离心率小于 ![]() 的椭圆的概率.
的椭圆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到下表中数据:
),得到下表中数据:
编号 |
|
|
|
|
|
|
|
|
长度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件长度相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com