【答案】
分析:根据题意,该程序框图的作用是计算S=-1
2+2
2-3
2+4
2-5
2+…+(-1)
kk
2的值,并在S≥2012时,输出下一个k的值.因此计算出这个和,并讨论程序中,S从小于2012到大于或等于2012这个过程中的运算及判断,即可得到本题的答案.
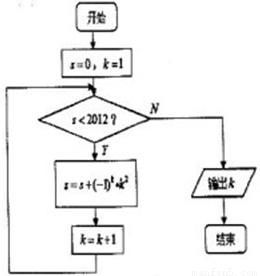
解答:解:根据题意,该程序框图的作用是
计算S=-1
2+2
2-3
2+4
2-5
2+…+(-1)
kk
2的值,并在S≥2012时,输出下一个k的值
①当k为偶数时,S=-1+4-9+16-…-(k-1)
2+k
2=3+7+…+(2k-1)=
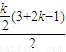
=
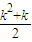
②当k为奇数时,S=-1+4-9+16-…+(k-1)
2-k
2=3+7+…+(2k-3)-k
2=
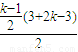
-k
2=-
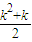
解不等式S<2012,得满足条件的最大正偶数k=62
k=62时,S=
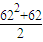
=1953,用k+1代替k,因为满足S<2012,用S-63
2代替S,并进入下一步;
k=63时,S=1953-63
2=-2016,并用k+1代替k,因为满足S<2012,用S+64
2代替S,进入下一步;
k=64时,S=-2016+64
2=2080,并用k+1代替k,因为不满足S<2012,结束循环体并输出最后的k值
因此,最后输出的k应该是65
故选D
点评:本题以循环型程序框图为载体,探索输出的k值,着重考查了循环语句和等差数列的求和公式等知识,属于基础题.

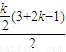 =
=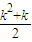
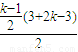 -k2=-
-k2=-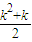
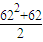 =1953,用k+1代替k,因为满足S<2012,用S-632代替S,并进入下一步;
=1953,用k+1代替k,因为满足S<2012,用S-632代替S,并进入下一步;
