
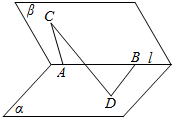
 如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.
如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3. 分析 由题设条件知 ${\overrightarrow{CD}}^{2}$=($\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$)2,由此利用向量法能求出CD的长.
解答 解:∵在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,AB=AC=2,CD=$\sqrt{11}$,
${\overrightarrow{CD}}^{2}$=($\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$)2=${\overrightarrow{CA}}^{2}$+${\overrightarrow{AB}}^{2}$+${\overrightarrow{BD}}^{2}$$+2\overrightarrow{CA}•\overrightarrow{AB}$+$2\overrightarrow{AB}•\overrightarrow{BD}$$+2\overrightarrow{CA}•\overrightarrow{BD}$
11=4+4+${\overrightarrow{BD}}^{2}$+0+0-2×$2×\left|\overrightarrow{BD}\right|×\frac{1}{2}$,
${\overrightarrow{BD}}^{2}$-$2\left|\overrightarrow{BD}\right|$-3=0,
解得$\left|\overrightarrow{BD}\right|$=3.
故答案为:3.
点评 本题考查线段长的求法,解题时要注意空间思维能力的培养,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | c>b>a | C. | a>b>c | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额X(元) | [500,1000) | [1000,1500) | [1500,+∞) |
| 抽奖次数 | 1 | 2 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 4 | C. | $\frac{1}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com