
 ,求:
,求: 中
中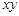 的最大值和最小值.
的最大值和最小值.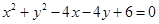 。 参数方程为:
。 参数方程为: 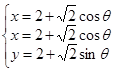 (
(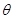 为参数) ;(2)最大值为:9,最小值为:1.
为参数) ;(2)最大值为:9,最小值为:1.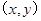 与极径
与极径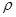 ,极角
,极角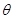 间的关系:
间的关系: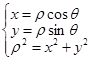 ,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点
,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点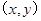 与圆半径
与圆半径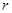 ,圆上点与圆心
,圆上点与圆心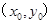 连线与
连线与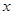 轴正向夹角
轴正向夹角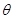 的关系:
的关系: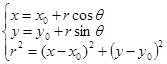 ;(2)利用圆的参数方程,将
;(2)利用圆的参数方程,将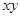 转化为关于
转化为关于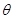 的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为
的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为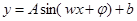 的形式),得到三角函数与二次函数的复合函数.
的形式),得到三角函数与二次函数的复合函数.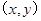 与极径
与极径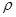 ,极角
,极角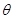 间的关系:
间的关系: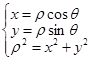 ,
,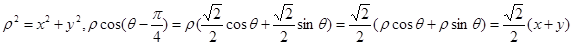 ,
,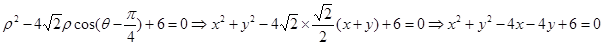
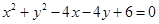 。 2分
。 2分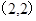 ,半径
,半径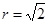
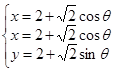 (
(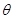 为参数) 。 4分
为参数) 。 4分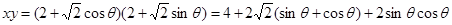 5分
5分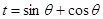 ,
,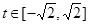 , 则
, 则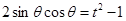 .
. 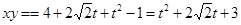 6分
6分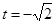 时,最小值是1; 8分
时,最小值是1; 8分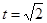 时,最大值是9. 10分
时,最大值是9. 10分

科目:高中数学 来源:不详 题型:解答题

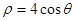 ,直线
,直线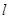 方程为
方程为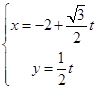 (t为参数),直线
(t为参数),直线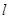 与C的公共点为T.
与C的公共点为T.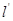 ,
,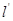 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线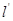 的极坐标方程.
的极坐标方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
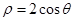 ,
,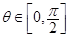 .
.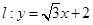 垂直,根据(1)中你得到的参数方程,确定D的坐标.
垂直,根据(1)中你得到的参数方程,确定D的坐标.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 3 |
A.(1,-
| B.(2,
| C.(2,-
| D.(2,-
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com