
【题目】已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
(1)当![]() 时,求不等式的解集A;
时,求不等式的解集A;
(2)若![]() ,试求不等式的解集B;
,试求不等式的解集B;
(3)设原不等式的解集为C,记![]() (其中
(其中![]() 为整数集),试探究集合M能否为有限集?若能,求出使得集合M中元素个数最少的实数
为整数集),试探究集合M能否为有限集?若能,求出使得集合M中元素个数最少的实数![]() 的所有取值,并用列举法表示集合M;若不能,请说明理由.
的所有取值,并用列举法表示集合M;若不能,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为6cm,该纸片上的正方形ABCD的中心为O.E,F,G,H为圆O上的点,△ABE,△BCF,△CDG,△ADH分别是以AB,BC,CD,DA为底边的等腰三角形.沿虚线剪开后,分别以AB,BC,CD,DA为折痕折起△ABE,△BCF,△CDG,△ADH,使得E,F,G,H重合得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.

问:(1)这个几何体是什么?
(2)这个几何体由几个面构成?每个面的三角形是什么三角形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速;
(3)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间.
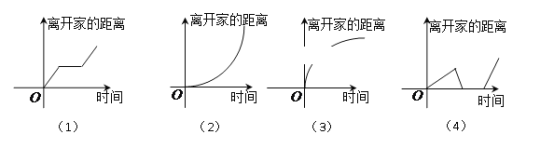
A. (1)(2)(4) B. (4)(2)(1) C. (4)(3)(1) D. (4)(1)(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com