
【题目】已知函数y=x3﹣3x+c的图象与x轴恰有两个公共点,则c=( )
A.﹣2或2
B.﹣9或3
C.﹣1或1
D.﹣3或1
【答案】A
【解析】解:求导函数可得y′=3(x+1)(x﹣1),
令y′>0,可得x>1或x<﹣1;令y′<0,可得﹣1<x<1;
∴函数在(﹣∞,﹣1),(1,+∞)上单调增,(﹣1,1)上单调减,
∴函数在x=﹣1处取得极大值,在x=1处取得极小值.
∵函数y=x3﹣3x+c的图象与x轴恰有两个公共点,
∴极大值等于0或极小值等于0.
∴1﹣3+c=0或﹣1+3+c=0,
∴c=﹣2或2.
故选:A.
【考点精析】利用函数的极值与导数和函数的零点与方程根的关系对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


科目:高中数学 来源: 题型:
【题目】设{an}是公比不为1的等比数列,其前n项和为Sn , 且a5 , a3 , a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+ , Sk+2 , Sk , Sk+1成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF. 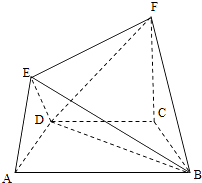
(1)求证:BD⊥平面AED;
(2)求二面角F﹣BD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若函数f(x)=ax2-x-1有且仅有一个零点, 求实数a的值.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体的所有棱长和为_______.
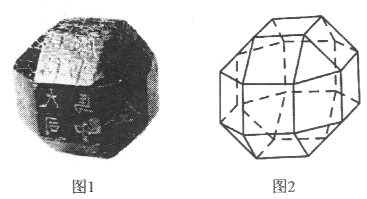
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.已知A= ![]() ,bsin(
,bsin( ![]() +C)﹣csin(
+C)﹣csin( ![]() +B)=a,
+B)=a,
(1)求证:B﹣C= ![]()
(2)若a= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com