
分析 用较大的数字除以较小的数字,得到商和余数,然后再用上一式中的除数和得到的余数中较大的除以较小的,以此类推,当整除时,就得到要求的最大公约数.先把5进制的数412(5)化为十进制数再变为七进制数,用除k取余法,即可得解.
解答 解:用辗转相除法求5280和12155的最大公约数,
12155=2×5280+1595
5280=3×1595+495
1595=3×495+110
495=4×110+55
110=2×55
5280和12155的最大公约数为55.
检验:12155-5280=6875,
6875-5280=1595,
5280-1595=3685,
3685-1595=2090,
2090-1595=495,
1595-495=1100,
1100-495=605,
605-495=110,
495-110=385,
385-110=275,
275-110=165,
165-110=55,
110-55=55.
经检验:5280和12155的最大公约数为55.
412(5)=2×50+1×51+4×52=2+5+4×25=107,
∵107=2×70+1×71+2×7 2
∴把5进制的数412(5)化为7进制是212(7).
点评 本题考查的知识点是辗转相除法,其中熟练掌握辗转相除法和更相减损术求两个正整数最大公约数的步骤是解答本题的关键.还考查进位制之间的换算,熟练掌握进行制的变化规律是正确解题的要诀.


科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
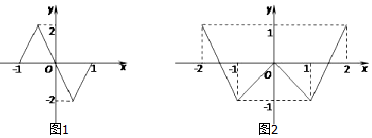
| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 625 | C. | 240 | D. | 1024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com