
如图,在边长为1的等边三角形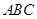 中,
中,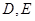 分别是
分别是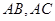 边上的点,
边上的点,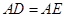 ,
,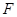 是
是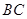 的中点,
的中点,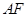 与
与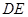 交于点
交于点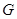 ,将
,将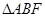 沿
沿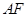 折起,得到如图所示的三棱锥
折起,得到如图所示的三棱锥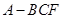 ,其中
,其中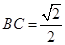 .
.
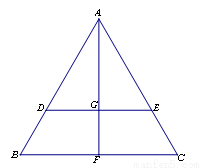
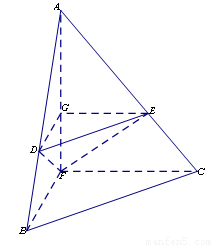
(1) 证明: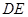 //平面
//平面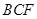 ;
;
(2) 证明: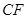
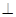 平面
平面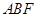 ;
;
(3) 当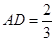 时,求三棱锥
时,求三棱锥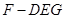 的体积
的体积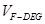 .
.
(1)见解析 (2) 见解析(3)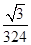
【解析】(1)在等边三角形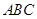 中,
中,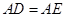
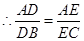 ,在折叠后的三棱锥
,在折叠后的三棱锥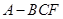 中
中
也成立, ,
,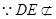 平面
平面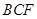 ,
,
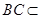 平面
平面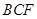 ,
,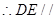 平面
平面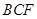 ;
;
(2)在等边三角形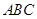 中,
中,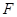 是
是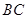 的中点,所以
的中点,所以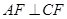 ①,
①,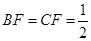 .
.
 在三棱锥
在三棱锥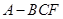 中,
中,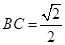 ,
,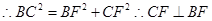 ②
②
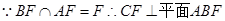 ;
;
(3)由(1)可知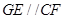 ,结合(2)可得
,结合(2)可得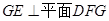 .
.
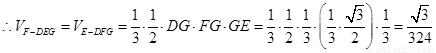
解决折叠问题,需注意一下两点:1.一定要关注“变量”和“不变量”在证明和计算中的应用:折叠时位于棱同侧的位置关系和数量关系不变;位于棱两侧的位置关系与数量关系变;2.折前折后的图形结合起来使用.本题第一问关键是利用相似比在折叠完以后没有变化,达到证明目的;第二问中借助勾股定理和不变的垂直关系,借助线面垂直的判断定理证明;第三问利用体积转化,充分借助第一问的平行关系和第二问的垂直关系进行求解.
【考点定位】线面平行于垂直、几何体的体积问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
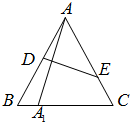 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,查看答案和解析>>
科目:高中数学 来源: 题型:044
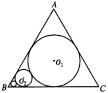
如图,在边长为1的等边△ABC中。圆O1为△ABC的内切圆。圆O2与圆O1外切,且与AB、BC相切……圆On-1,与圆On外切,且与AB、BC相切,如此无限继续下去,记圆On的面积为an(n∈N)。
(1)证明:{an}是等比数列;
(2)求![]() (a1+a2+a3+…+an)的值。
(a1+a2+a3+…+an)的值。
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一3月月考数学试卷(解析版) 题型:解答题
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
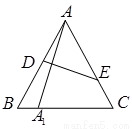
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
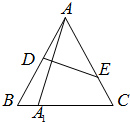 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com