
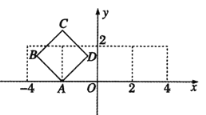
【题目】在平面直角坐标系![]() 中,如图放置的边长为2的正方形ABCD沿
中,如图放置的边长为2的正方形ABCD沿![]() 轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点
轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
A.函数![]() 在
在![]() 上有两个零点
上有两个零点
B.函数![]() 是偶函数
是偶函数
C.函数![]() 在
在![]() 上单调递增
上单调递增
D.对任意的![]() ,都有
,都有![]()
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是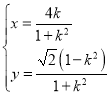 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎正在全球蔓延,对世界经济影响严重,中国疫情防控,复工复学恢复经济成为各国的榜样,绵阳某商场在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有2种服装商品的概率;
(2)商场对选的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高300元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金,假设顾客每次抽奖时获奖与否是等概率的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计某射击运动员随机射击一次命中目标的概率为![]() ,为估计该运动员射击4次恰好命中3次的概率,现采用随机模拟的方法,先由计算机产生0到9之间取整数值的随机数,用0,1,2表示没有击中,用3,4,5,6,7,8,9表示击中,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
,为估计该运动员射击4次恰好命中3次的概率,现采用随机模拟的方法,先由计算机产生0到9之间取整数值的随机数,用0,1,2表示没有击中,用3,4,5,6,7,8,9表示击中,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
9597,7424,7610,4281,7520,0293,7140,9857,0347,4373,
0371,6233,2616,8045,6011,3661,8638,7815,1457,5550.
根据以上数据,则可估计该运动员射击4次恰有3次命中的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是
是![]() 与
与![]() 的一个交点,其极坐标为
的一个交点,其极坐标为![]() .设射线
.设射线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com