
【题目】已知函数f(x)=2x,x∈R.
(1)当m取何值时,方程|f(x)-2|=m有一个解?两个解?
(2)若不等式[f(x)]2+f(x)-m>0在R上恒成立,求m的取值范围.
【答案】(1)当m=0或m≥2时,方程有一个解;当0<m<2时,方程有两个解.(2)m的取值范围为(-∞,0]。
【解析】
(1)有一个解、两个解问题,转化成F(x)=|f(x)-2|与G(x)=m有一个交点还是两个交点问题;
(2)不等式[f(x)]2+f(x)-m>0在R上恒成立,即4x+2x-m>0在R上恒成立,利用参变量分离法,转化成求4x+2x的取值范围.
(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示.

由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,原方程有一个解;
当0<m<2时,函数F(x)与G(x)的图象有两个交点,原方程有两个解.
(2)令f(x)=t(t>0),t=2x,则H(t)=t2+t,(t>0)
因为H(t)=![]() -
-![]() 在区间(0,+∞)上是增函数,
在区间(0,+∞)上是增函数,
所以H(t)>H(0)=0.
因此要使t2+t>m在区间(0,+∞)上恒成立,
应有m≤0,
即所求m的取值范围为(-∞,0].


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】观察下列三角形数表: 
假设第n行的第二个数为 ![]() ,
,
(1)归纳出an+1与an的关系式,并求出an的通项公式;
(2)设anbn=1(n≥2),求证:b2+b3+…+bn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若D′是平面α外一点,则下列命题正确的是( )
A.过D′只能作一条直线与平面α相交
B.过D′可作无数条直线与平面α垂直
C.过D′只能作一条直线与平面α平行
D.过D′可作无数条直线与平面α平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{bn}的前n项和为Sn , 且对任意正整数n,都有2Sn=bn(bn+1).
(1)求数列{bn}的通项公式;
(2)如果等比数列{an}共有2015项,其首项与公比均为2,在数列{an}的每相邻两项ak与ak+1之间插入k个(﹣1)kbk(k∈N*)后,得到一个新的数列{cn}.求数列{cn}中所有项的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,求实数λ的范围.
成立,求实数λ的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线x﹣9y﹣8=0与曲线C:y=x3﹣px2+3x相交于A,B,且曲线C在A,B处的切线平行,则实数p的值为( )
A.4
B.4或﹣3
C.﹣3或﹣1
D.﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: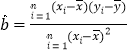 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API | [0,100] | (100,200] | (200,300] | >300 |
空气质量 | 优良 | 轻污染 | 中度污染 | 重度污染 |
天数 | 17 | 45 | 18 | 20 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为![]() .当
.当![]() 时,企业没有造成经济损失;当
时,企业没有造成经济损失;当![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 时造成的经济损失为
时造成的经济损失为![]() ,当
,当![]() 时,造成的经济损失
时,造成的经济损失![]() );当
);当![]() 时造成的经济损失为2000元;
时造成的经济损失为2000元;
(1)试写出![]() 的表达式;
的表达式;
(2)若本次抽取的样本数据有30天是在供暖季,其中有12天为重度污染,完成下面2×2列联表,并判断能否有99%的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
![]()
P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com