③
分析:对于命题①,直接求积分即可判断真假;命题②是全称命题的否定,全称命题的否定是特称命题,由此可判断命题②的真假;命题③由x>2能推出x>1,但由x>1不能推出x>2;命题④考查了向量在向量上的投影,首先求出给出的两个向量的数量积,再求出向量

的模,则

在

上的投影可求;命题⑤首先对复合函数求导,根据导函数的最大值是3求出ω的值,的导函数解析式后把

代入函数解析式验证,函数能取最大值则是对称轴,否则不是.
解答:
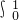
(1-e
x)dx=

=1-(e
1-e
0)=2-e,∴命题①错误;
命题“?x>3,x
2+2x+1>0”的否定是“?x>3,x
2+2x+1≤0”,∴命题②错误;
由x>2,一定有x>1,反之,由x>1,不一定有x>2,如x=

.
∴“x>2”是“x>1”的充分不必要条件,∴命题③正确;
由
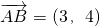
,

=(-2,-1),设

与

的夹角为θ,
则
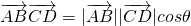
=3×(-2)+4×(-1)=-10,
∵
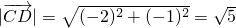
,∴
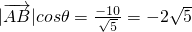
.
∴

在

上的投影为
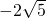
.∴命题④错误;
由f(x)=sin(ωx+

)-2,则f
′(x)=ω•cos(ωx

),
∵函数
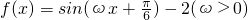
的导函数的最大值为3,∴ω=3.
则f(x)=sin(3x+

)-2,而
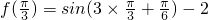
=

>-3,∴函数f(x)的图象不关于

对称.
∴命题⑤错误.
所以正确的命题为③.
故答案为③.
点评:本题考查了命题的真假判断与应用,考查了微积分基本定理,训练了复合函数的求导法则,正确理解向量在向量上的投影是解答该题的关键,此题是中档题.

 (1-ex)dx=1-e;
(1-ex)dx=1-e;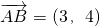 ,
, =(-2,-1),则
=(-2,-1),则 在
在 上的投影为-2;
上的投影为-2;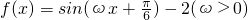 的导函数的最大值为3,则函数f(x)的图象关于
的导函数的最大值为3,则函数f(x)的图象关于 对称,
对称, 的模,则
的模,则 在
在 上的投影可求;命题⑤首先对复合函数求导,根据导函数的最大值是3求出ω的值,的导函数解析式后把
上的投影可求;命题⑤首先对复合函数求导,根据导函数的最大值是3求出ω的值,的导函数解析式后把 代入函数解析式验证,函数能取最大值则是对称轴,否则不是.
代入函数解析式验证,函数能取最大值则是对称轴,否则不是. (1-ex)dx=
(1-ex)dx= =1-(e1-e0)=2-e,∴命题①错误;
=1-(e1-e0)=2-e,∴命题①错误; .
.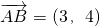 ,
, =(-2,-1),设
=(-2,-1),设 与
与 的夹角为θ,
的夹角为θ,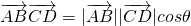 =3×(-2)+4×(-1)=-10,
=3×(-2)+4×(-1)=-10,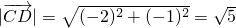 ,∴
,∴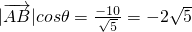 .
. 在
在 上的投影为
上的投影为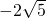 .∴命题④错误;
.∴命题④错误; )-2,则f′(x)=ω•cos(ωx
)-2,则f′(x)=ω•cos(ωx ),
),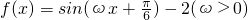 的导函数的最大值为3,∴ω=3.
的导函数的最大值为3,∴ω=3. )-2,而
)-2,而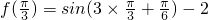 =
= >-3,∴函数f(x)的图象不关于
>-3,∴函数f(x)的图象不关于 对称.
对称.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案![]() ;②若函数
;②若函数![]() ,则f(x)是周期函数;③如图,二面角
,则f(x)是周期函数;③如图,二面角![]() 的大小是45°,线段
的大小是45°,线段![]() .
.![]() ,
,![]() 与
与![]() 所成的角为30°.则
所成的角为30°.则![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是
;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是![]() ;其中正确的是 ;⑤已知
;其中正确的是 ;⑤已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 夹角的最大值是
夹角的最大值是![]() 。
。