
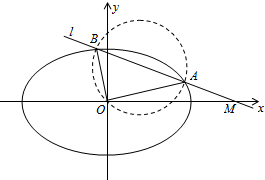
分析 设直线l的方程,代入椭圆方程,消去y,整理得(1+k2)x2-4k2x+4k2-2=0,以线段AB的圆经过坐标原点O,可得x1x2+y1y2=0,利用韦达定理,求出k,即可求直线l的方程.
解答 解:设直线l的方程为y=k(x-2),代入椭圆方程,消去y,整理得(1+k2)x2-4k2x+4k2-2=0.
设A(x1,y1)、B(x2,y2),则x1+x2=$\frac{4{k}^{2}}{1+{k}^{2}}$,x1x2=$\frac{4{k}^{2}-2}{1+{k}^{2}}$,
∴y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]=$\frac{2{k}^{2}}{1+{k}^{2}}$,
∵以线段AB的圆经过坐标原点O,
∴x1x2+y1y2=0,即$\frac{4{k}^{2}-2}{1+{k}^{2}}$+$\frac{2{k}^{2}}{1+{k}^{2}}$=0
解得k=±1.
∴所求直线l的方程为y=±(x-2).
点评 本题考查直线方程,考查直线与椭圆的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.


科目:高中数学 来源: 题型:选择题
| A. | 一个四边形的4个顶点 | |
| B. | 过一个定点,且与两条异面直线垂直 | |
| C. | 过平面外一个定点,且与这个平面平行 | |
| D. | 过平面外一个定点,且与这个平面垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
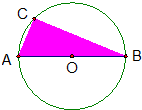 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )| A. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2π}$ | B. | $\frac{π}{3}$,$\frac{\sqrt{3}}{2π}$ | C. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{6}$,$\frac{3}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com