
【题目】如图,在四棱锥P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分别为PD,BD的中点,且![]() .
.
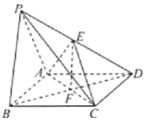
(1)求证:平面PAD⊥平面ABCD;
(2)求锐二面角E-AC-D的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先过P作PO⊥AD,再通过平几知识计算得PO⊥BO,利用线面垂直判定定理得PO⊥平面ABCD,再根据面面垂直判定定理得结果,(2)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面ACE的一个法向量,根据向量数量积得向量夹角,最后根据二面角与向量夹角关系得结果.
(1)过P作PO⊥AD,垂足为O,连结AO,BO,
由∠PAD=120°,得∠PAO=60°,
∴在Rt△PAO中,PO=PAsin∠PAO=2sin60°=2×![]() =
=![]() ,
,
∵∠BAO=120°,∴∠BAO=60°,AO=AO,∴△PAO≌△BAO,∴BO=PO=![]() ,
,
∵E,F分别是PA,BD的中点,EF=![]() ,∴EF是△PBD的中位线,
,∴EF是△PBD的中位线,
∴PB=2EF=2×![]() =
=![]() ,
,
∴PB2=PO2+BO2,∴PO⊥BO,∵AD∩BO=O,∴PO⊥平面ABCD,
又PO平面PAD,∴平面PAD⊥平面ABCD.
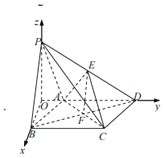
(2)以O为原点,OB为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,
A(0,1,0),P(0,0,![]() ),B(
),B(![]() ,0,0),D(0,3,0),
,0,0),D(0,3,0),
∴E(0,![]() ),F(
),F(![]() ,
,![]() ),
),![]() =(0,
=(0,![]() ),
),![]() =(
=(![]() ,
,![]() ,0),
,0),
易得平面ABCD的一个法向量![]() =
=
设平面ACE的法向量![]() =(x,y,z),则
=(x,y,z),则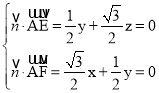 ,
,
取x=1,得![]() =(1,-
=(1,-![]() ,1),
,1),
设锐二面角的平面角的大小为θ,则cosθ=|cos<![]() >|=
>|=![]() =
=![]() ,
,
∴锐二面角E-AC-D的余弦值为![]() .
.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人各自独立的参加某单位面试,规定每位考生需要从编号为1-6的6道面试题中随机抽出3道进行面试,至少答对两道才能合格.已知甲能答对其中3道题,乙能答对其中4道题.
(1)求甲恰好答对两道题的概率.
(2)求甲合格且乙不合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若动点P到点F(0,1)的距离比它到直线y=﹣2的距离少1,则动点P的轨迹C的方程为_____,若过点(2,1)作该曲线C的切线l,则切线l的方程为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数f(x)=ax2﹣2bx+8.
(1)设集合P={1,2,3}和Q={2,3,4,5},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
(2)设集合P=[1,3]和Q[2,5],分别从集合P和Q中随机取一个实数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x的焦点为F,过点F且斜率为1的直线与抛物线C交于A、B两点,若在以线段AB为直径的圆上存在两点M、N,在直线![]() :x+y+a=0上存在一点Q,使得∠MQN=90°,则实数a的取值范围为( )
:x+y+a=0上存在一点Q,使得∠MQN=90°,则实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,t为参数直线
,t为参数直线![]() 与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线
与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4一4:坐标系与参数方程
在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心的极坐标为(
是圆心的极坐标为(![]() )且经过极点的圆
)且经过极点的圆
(1)求曲线C1的极坐标方程和C2的普通方程;
(2)已知射线![]() 分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com