
 .
. ;(提示:可先求证
;(提示:可先求证 (i=1,2,…,n-1),然后再完成所要证的结论.)
(i=1,2,…,n-1),然后再完成所要证的结论.)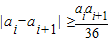 (i=1,2,…,n-1),由此能够推导出
(i=1,2,…,n-1),由此能够推导出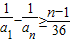 .
.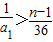 ,a1≥1,得
,a1≥1,得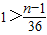 ,导出n<37.由此能够推导出
,导出n<37.由此能够推导出 ,从而能够证明n≤11.
,从而能够证明n≤11.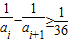 ,
,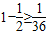 ,
,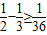 ,
,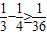 ,
,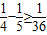 ,
,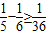 ,设a1=1,a2=2,a3=3,a4=4,a5=5,a6=6,由此能够推导出满足条件的一个集合A.
,设a1=1,a2=2,a3=3,a4=4,a5=5,a6=6,由此能够推导出满足条件的一个集合A. (i=1,2,…,n-1),
(i=1,2,…,n-1),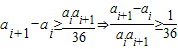 ,
,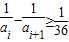 (i=1,2,…,n-1).…(2分)
(i=1,2,…,n-1).…(2分)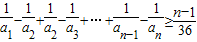 ,
,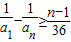 .…(4分)
.…(4分)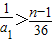 ,
,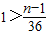 ,因此n<37.…(5分)
,因此n<37.…(5分)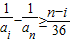 ,知
,知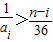 .又ai≥i,得
.又ai≥i,得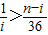 .…(7分)
.…(7分)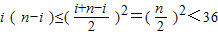 ,符合题意,
,符合题意,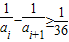 ,
,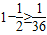 ,
,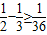 ,
,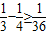 ,
,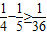 ,
,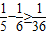 ,
,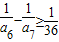 ,可得
,可得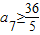 ,取a7=8;…(13分)
,取a7=8;…(13分) ,可得
,可得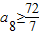 ,取a8=11;…(14分)
,取a8=11;…(14分)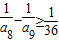 ,可得
,可得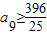 ,取a9=16;…(15分)
,取a9=16;…(15分)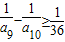 ,可得
,可得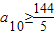 ,取a10=29;…(16分)
,取a10=29;…(16分)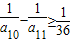 ,可得
,可得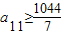 ,取a11=150;…(17分)
,取a11=150;…(17分)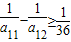 ,得
,得 ,
,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
| xy |
| 25 |
| 1 |
| a1 |
| 1 |
| an |
| n-1 |
| 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n(n-1) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| xy |
| 36 |
| 1 |
| a1 |
| 1 |
| an |
| n-1 |
| 36 |
| 1 |
| ai |
| 1 |
| ai+1 |
| 1 |
| 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com