
【题目】已知抛物线E:![]() 焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且
焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且![]() .
.
(1)求抛物线E的方程;
(2)设O是坐标原点,P,Q是抛物线E上分别位于x轴两侧的两个动点,且![]()
①证明:直线PQ必过定点,并求出定点G的坐标;
②过G作PQ的垂线交抛物线于C,D两点,求四边形PCQD面积的最小值.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x﹣4y+m=0.
(1)若圆C与直线l:x+2y﹣4=0相交于M、N两点,且|MN|![]() ,求m的值;
,求m的值;
(2)在(1)成立的条件下,过点P(2,1)引圆的切线,求切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船一天的捕鱼量的平均数;
的渔船一天的捕鱼量的平均数;
(Ⅱ)若以(Ⅰ)中确定的平均数作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①估计一艘上述吨位的捕鱼船一年在捕鱼期内的捕鱼总量;
②已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘;若不捕鱼,每天成本为2万元/艘,请依据往年天气统计数据,估计一艘此种捕鱼船年利润不少于1600万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,一个焦点为
,一个焦点为![]() .
.
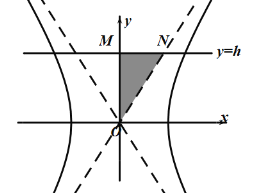
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上的任意一点
上的任意一点![]() ,分别作这两条渐近线的平行线与这两条渐近线得到四边形
,分别作这两条渐近线的平行线与这两条渐近线得到四边形![]() ,证明四边形
,证明四边形![]() 的面积是一个定值;
的面积是一个定值;
(3)设直线![]() 与
与![]()
![]() 在第一象限内与渐近线
在第一象限内与渐近线![]() 所围成的三角形
所围成的三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体的体积.
轴旋转一周所得几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆的左、右焦点,过右焦点
为椭圆的左、右焦点,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点A是第一象限内椭圆上一点,且在![]() 轴上的正投影为右焦点
轴上的正投影为右焦点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交椭圆于
分别交椭圆于![]() 两点,当直线
两点,当直线![]() 的倾斜角互补时,试问:直线
的倾斜角互补时,试问:直线![]() 的斜率是否为定值;若是,请求出其定值;否则,请说明理由.
的斜率是否为定值;若是,请求出其定值;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
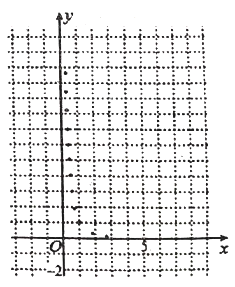
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为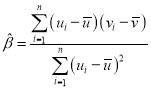 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com