
【题目】已知函数![]()
![]() 是
是![]() 的一个极值点.
的一个极值点.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间为(﹣∞,1),(2,+∞);单调减区间为(1,2).(2)0<a<1.
【解析】
(1)求导函数,利用f'(2),可求b的值,进而利用f'(x)>0可得函数f(x)的单调增区间,f'(x)<0可得函数f(x)的单调减区间;
(2)x∈[1,+∞)时,![]() 恒成立等价于
恒成立等价于![]() ,由此可求a的取值范围.
,由此可求a的取值范围.
(1)求导函数,可得f'(x)=x2﹣2bx+2
∵x=2是f(x)的一个极值点
∴f'(2)=4﹣4b+2=0,∴![]() ,∴f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
,∴f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
由f'(x)>0得x>2或x<1,∴函数f(x)的单调增区间为(﹣∞,1),(2,+∞);
由f'(x)<0得1<x<2,∴函数f(x)的单调减区间为(1,2).
(2)由(1)知,函数f(x)在(1,2)上单调递减,在(2,+∞)上单调递增
∴当x=2时,函数f(x)取得最小值,f(x)min=f(2)![]() ,
,
x∈[1,+∞)时,![]() 恒成立等价于
恒成立等价于![]()
即a2﹣a<0,
∴0<a<1.


科目:高中数学 来源: 题型:
【题目】在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)试在棱![]() (不包含端点
(不包含端点![]() )上确定一点
)上确定一点![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求![]() 和平面
和平面![]() 所成角正弦值的大小.
所成角正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图。下面关于这两位同学的数学成绩的分析中,正确的共有( )个。

①甲同学的成绩折线图具有较好的对称性,与正态曲线相近,故而平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与考试次号具有比较明显的线性相关性,且为正相关;
④乙同学在这连续九次测验中的最高分与最低分的差超过40分。
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
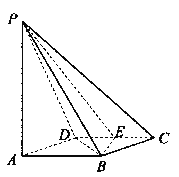
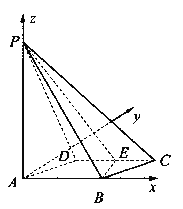
【题目】如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,
E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)证明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.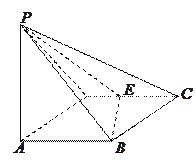
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列对各事件发生的概率判断正确的是( )
A.某学生在上学的路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是![]() ,那么该生在上学路上到第3个路口首次遇到红灯的概率为
,那么该生在上学路上到第3个路口首次遇到红灯的概率为![]()
B.三人独立地破译一份密码,他们能单独译出的概率分别为![]() ,
,![]() ,
,![]() ,假设他们破译密码是彼此独立的,则此密码被破译的概率为
,假设他们破译密码是彼此独立的,则此密码被破译的概率为![]()
C.甲袋中有8个白球,4个红球,乙袋中有6个白球,6个红球,从每袋中各任取一个球,则取到同色球的概率为![]()
D.设两个独立事件A和B都不发生的概率为![]() ,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率是
,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于15小时,也不超过40小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一张长为80cm、宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面正方形边长为x(cm),高为y(cm),体积为V(cm3).求:
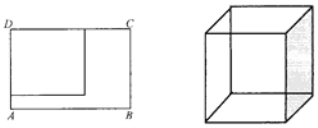
(1)y关于x的表达式;
(2)该铁皮盒体积V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李独立参加每次考核合格的概率依次组成一个公差为![]() 的等差数列,他参加第一次考核合格的概率不超过
的等差数列,他参加第一次考核合格的概率不超过![]() ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为![]() .
.
(1)求小李第一次参加考核就合格的概率![]() ;
;
(2)求小李参加考核的次数![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com