
分析 先求出基本事件总数n=6×6=36,再求出小明掷出的点数不大于2或小红掷出的点数不小于3包含的基本事件个数m=2×6+6×4-2×4=28,由此能求出小明掷出的点数不大于2或小红掷出的点数不小于3的概率.
解答 解:小明和小红各自掷一颗均匀的正方体骰子,两人相互独立地进行,
基本事件总数n=6×6=36,
小明掷出的点数不大于2或小红掷出的点数不小于3包含的基本事件个数:
m=2×6+6×4-2×4=28,
∴小明掷出的点数不大于2或小红掷出的点数不小于3的概率为:
p=$\frac{m}{n}=\frac{28}{36}$=$\frac{7}{9}$.
故答案为:$\frac{7}{9}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | 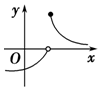 | B. | 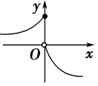 | C. | 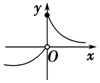 | D. | 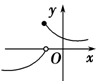 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
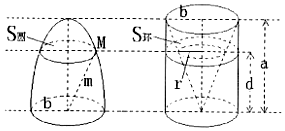 已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.
已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象M关于直线x=-$\frac{π}{12}$对称 | |
| B. | 由y=2sin2x的图象向左平移$\frac{π}{6}$得到M | |
| C. | 图象M关于点(-$\frac{π}{12}$,0)对称 | |
| D. | f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{12}$)上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (24,25) | B. | (18,24) | C. | (21,24) | D. | (18,25) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:解答题
已知f(x)=3x2-2x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=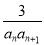 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<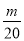 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com