
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)求![]() 的极值;
的极值;
(2)当![]() 在什么范围内取值时,曲线
在什么范围内取值时,曲线![]() 与
与![]() 轴仅有一个交点?
轴仅有一个交点?
【答案】(1)极大值是![]() ,极小值是
,极小值是![]() .(2)
.(2)![]()
【解析】试题分析:
(1)首先求得导函数,然后列表考查函数的单调性,据此可得f(x)的极大值是f(-![]() )=
)=![]() +a,极小值是f(1)=a-1.
+a,极小值是f(1)=a-1.
(2)由题意结合(1)中的极值的结论可得实数a的取值范围是![]() .
.
试题解析:
(1)f′(x)=3x2-2x-1.
令f′(x)=0,则x=-![]() 或x=1.
或x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (-∞,- | - | (- | 1 | (1,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以f(x)的极大值是f(-![]() )=
)=![]() +a,
+a,
极小值是f(1)=a-1.
(2)函数f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1,
由此可知,x取足够大的正数时,
有f(x)>0,x取足够小的负数时,有f(x)<0,
曲线y=f(x)与x轴至少有一个交点.
由(1)知f(x)极大值=f(-![]() )=
)=![]() +a,
+a,
f(x)极小值=f(1)=a-1.
∵曲线y=f(x)与x轴仅有一个交点,
∴f(x)极大值<0或f(x)极小值>0,
即![]() +a<0或a-1>0,
+a<0或a-1>0,
∴a<-![]() 或a>1,
或a>1,
∴当a∈(-∞,-![]() )∪(1,+∞)时,曲线y=f(x)与x轴仅有一个交点.
)∪(1,+∞)时,曲线y=f(x)与x轴仅有一个交点.


科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的月固定成本为10(万元),每生产![]() 件,需另投入成本为
件,需另投入成本为![]() (万元).当月产量不足30件时,
(万元).当月产量不足30件时, ![]() (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, ![]() (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)当月产量为多少件时,该厂所获月利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,已知第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只进行两道程序就停止审核的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求X的分布列及数学期望.
,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个学生在一次竞赛中要回答![]() 道题是这样产生的:从
道题是这样产生的:从![]() 道物理题中随机抽取
道物理题中随机抽取![]() 道;从
道;从![]() 道化学题中随机抽取
道化学题中随机抽取![]() 道;从
道;从![]() 道生物题中随机抽取
道生物题中随机抽取![]() 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为![]() ,化学题的编号为
,化学题的编号为![]() ,生物题的编号为
,生物题的编号为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
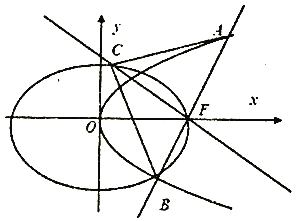
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com