
| 正常 | 非正常 | 合计 | |
| 男 | 30 | 20 | 50 |
| 女 | 50 | 10 | 60 |
| 合计 | 80 | 30 | 110 |
| P(K2≥k0) | 0.100 | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (Ⅰ)在调查对象中随机抽取1人,为非正常消费的概率为$\frac{3}{11}$,可得非正常消费的人数,即可得到列联表;
(Ⅱ)利用公式求得K2,与临界值比较,即可得到结论.
解答 解:(Ⅰ)
| 正常 | 非正常 | 合计 | |
| 男 | 30 | 20 | 50 |
| 女 | 50 | 10 | 60 |
| 合计 | 80 | 30 | 110 |
点评 根据所给的列联表得到求观测值所用的数据,把数据代入观测值公式中,做出观测值,同所给的临界值表进行比较,得到所求的值所处的位置,得到百分数.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$或1 | C. | 1或$\frac{1}{2}$ | D. | $\frac{1}{2}$或$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
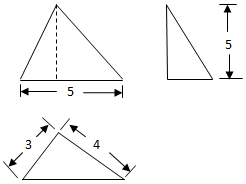
| A. | $4\sqrt{2}$ | B. | $\sqrt{34}$ | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 有无数解 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>e2 | B. | a<e2 | C. | a>-2e | D. | a<-2e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{e^π}(1-{e^{2017π}})}}{{1-{e^{2π}}}}$ | B. | $\frac{{{e^π}(1-{e^{1009π}})}}{{1-{e^π}}}$ | ||
| C. | $\frac{{{e^π}(1-{e^{1008π}})}}{{1-{e^{2π}}}}$ | D. | $\frac{{{e^π}(1-{e^{2016π}})}}{{1-{e^{2π}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com