解:(1)求导函数可得f′(x)=3x
2+2bx+c
∵函数f(x)在区间(-∞,-2]上单调递增,在区间
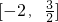
上单调递减,
∴f′(-2)=12-4b+c=0,即c=4b-12…(3分)
∵

,∴28b-21≤0,∴
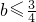
∵b是非负整数,∴b=0,…(6分)
从而c=12,所以f(x)=x
3-12x+1…(8分)
(2)求导数f′(x)=3(x+2)(x-2),则f(x)在[-2,2]上单调递减,在[2,+∞)上单调递增
∵0<m≤2,∴-2<m-2≤0,∴f(x)在[m-2,m]上单调递减
∴[f(x)]
max=f(m-2),[f(x)]
min=f(m)…(12分)
依题意[f(x)]
max-[f(x)]
min≤16m,即3m
2+2m-8≥0
∴m≤-2或m≥

∵0<m≤2,∴
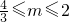
∴m的最小值为

…(16分)
分析:(1)求导函数,利用函数f(x)在区间(-∞,-2]上单调递增,在区间
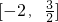
上单调递减,可得f′(-2)=0,

,结合b是非负整数,可得f(x)的表达式;
(2)若对任意的t
1,t
2∈[m-2,m],不等式|f(t
1)-f(t
2)|≤16m恒成立,等价于[f(x)]
max-[f(x)]
min≤16m,求出函数的最值,即可确定m的取值范围,从而可得m的最小值.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查恒成立问题,正确运用函数的单调性是关键.

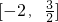 上单调递减,若b是非负整数
上单调递减,若b是非负整数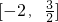 上单调递减,
上单调递减, ,∴28b-21≤0,∴
,∴28b-21≤0,∴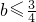

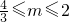
 …(16分)
…(16分)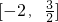 上单调递减,可得f′(-2)=0,
上单调递减,可得f′(-2)=0, ,结合b是非负整数,可得f(x)的表达式;
,结合b是非负整数,可得f(x)的表达式;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<