
【题目】如图,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,过点(0,﹣b),(a,0)的直线与原点的距离为
,过点(0,﹣b),(a,0)的直线与原点的距离为 ![]() ,M(x0 , y0)是椭圆上任一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=2作两条切线,分别交椭圆于点P,Q.
,M(x0 , y0)是椭圆上任一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=2作两条切线,分别交椭圆于点P,Q.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若记直线OP,OQ的斜率分别为k1 , k2 , 试求k1k2的值.
【答案】解:(Ⅰ)由椭圆的离心率e= ![]() =
= ![]() =
= ![]() ,
,
即a2=2b2 , ①
设过点(0,﹣b),(a,0)的直线方程为 ![]() ,
,
即bx﹣ay﹣ab=0,
因为直线与原点的距离为 ![]() ,
,
∴ ![]() =
= ![]() ,整理得:
,整理得: ![]() =2,②
=2,②
由①②得 ![]() ,
,
∴椭圆的方程为 ![]() ;
;
(Ⅱ)由直线OP:y=k1x,OQ:y=k2x,与圆M相切,
由直线和圆相切的条件:d=r,可得 ![]() =
= ![]() =
= ![]() ,
,
平方整理,可得k12(2﹣x02)+2k1x0y0+2﹣y02=0,
k22(2﹣x02)+2k2x0y0+2﹣y02=0,
∴k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的两个不相等的实数根,
k1k2= ![]() ,
,
由点R(x0 , y0)在椭圆C上,
∴ ![]() ,即y02=3(1﹣
,即y02=3(1﹣ ![]() )=3﹣
)=3﹣ ![]() x02 ,
x02 ,
∴k1k2= ![]() =﹣
=﹣ ![]() ,
,
k1k2的值为﹣ ![]() .
.
【解析】(Ⅰ)由椭圆的离心率公式可知a2=2b2 , 利用点到直线的距离公式 ![]() =2,即可求得a和b的值,即可求得椭圆方程;(Ⅱ)利用点到直线的距离公式,可知k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的两个不相等的实数根,利用韦达定理即可求得k1k2 , 由R(x0 , y0)在椭圆C上,y02=3﹣
=2,即可求得a和b的值,即可求得椭圆方程;(Ⅱ)利用点到直线的距离公式,可知k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的两个不相等的实数根,利用韦达定理即可求得k1k2 , 由R(x0 , y0)在椭圆C上,y02=3﹣ ![]() x02 , 代入即可求得k1k2的值.
x02 , 代入即可求得k1k2的值.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)= 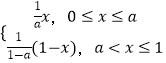 ,a为常数,且a∈(0,1).
,a为常数,且a∈(0,1).
(1)若x0满足f(x0)=x0 , 则称x0为f(x)的一阶周期点,证明函数f(x)有且只有两个一阶周期点;
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶周期点,当a= ![]() 时,求函数f(x)的二阶周期点.
时,求函数f(x)的二阶周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈(0, ![]() ))的图象在y轴上的截距为1,在相邻两个最值点
))的图象在y轴上的截距为1,在相邻两个最值点 ![]() 和(x0 , ﹣2)上(x0>0),函数f(x)分别取最大值和最小值.
和(x0 , ﹣2)上(x0>0),函数f(x)分别取最大值和最小值.
(1)求函数f(x)的解析式;
(2)若f(x)= ![]() 在区间
在区间 ![]() 内有两个不同的零点,求k的取值范围;
内有两个不同的零点,求k的取值范围;
(3)求函数f(x)在区间 ![]() 上的对称轴方程.
上的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a、b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点 ![]() 对称
对称
C.奇函数且它的图象关于点 ![]() 对称
对称
D.奇函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)求函数f(x)的单调区间;
(3)若函数 ![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且2asinB﹣ ![]() bcosA=0.
bcosA=0.
(1)求cosA;
(2)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com