
分析 (Ⅰ)设点设P(x0,y0),从而可得直线PA与PB的斜率乘积为$\frac{y_0}{{{x_0}+\sqrt{3}}}×\frac{y_0}{{{x_0}-\sqrt{3}}}=\frac{y_0^2}{x_0^2-3}=\frac{6-2x_0^2}{3(x_0^2-3)}=-\frac{2}{3}$
(Ⅱ)设方程为y=kx+m,由两点M,N满足OM∥PA,ON∥PB及(Ⅰ)得直线OM,ON的斜率乘积为-$\frac{2}{3}$,可得到m、k的关系,再用弦长公式及距离公式,求出△OMN的底、高,表示:△OMN的面积即可.
解答 (本小题满分13分)
解:(Ⅰ)证明:设P(x0,y0),则$\frac{{{x_0}^2}}{3}+\frac{{{y_0}^2}}{2}=1$.
所以直线PA与PB的斜率乘积为$\frac{y_0}{{{x_0}+\sqrt{3}}}×\frac{y_0}{{{x_0}-\sqrt{3}}}=\frac{y_0^2}{x_0^2-3}=\frac{6-2x_0^2}{3(x_0^2-3)}=-\frac{2}{3}$.…(4分)
(Ⅱ)依题直线OM,ON的斜率乘积为$-\frac{2}{3}$.
①当直线MN的斜率不存在时,直线OM,ON的斜率为$±\frac{{\sqrt{6}}}{3}$,设直线OM的方程
是$y=\frac{{\sqrt{6}}}{3}x$,由$\left\{{\begin{array}{l}{2{x^2}+3{y^2}=6}\\{y=\frac{{\sqrt{6}}}{3}x}\end{array}}\right.$得$x=±\frac{{\sqrt{6}}}{2}$,y=±1.
取$M(\frac{{\sqrt{6}}}{2},1)$,则$N(\frac{{\sqrt{6}}}{2},-1)$.所以△OMN的面积为$\frac{{\sqrt{6}}}{2}$.
②当直线MN的斜率存在时,设直线MN的方程是y=kx+m,
由$\left\{{\begin{array}{l}{y=kx+m}\\{2{x^2}+3{y^2}-6=0}\end{array}}\right.$得(3k2+2)x2+6kmx+3m2-6=0.
因为M,N在椭圆C上,
所以△=36k2m2-4(3k2+2)(3m2-6)>0,解得3k2-m2+2>0.
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=-\frac{6km}{{3{k^2}+2}}$,${x_1}{x_2}=\frac{{3{m^2}-6}}{{3{k^2}+2}}$.$|{MN}|=\sqrt{({k^2}+1)[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}]}=\sqrt{({k^2}+1)[{{(\frac{-6km}{{3{k^2}+2}})}^2}-4×\frac{{3{m^2}-6}}{{3{k^2}+2}}]}$=$2\sqrt{\frac{{6({k^2}+1)(3{k^2}-{m^2}+2)}}{{{{(3{k^2}+2)}^2}}}}$.
设点O到直线MN的距离为d,则$d=\frac{|m|}{{\sqrt{{k^2}+1}}}$.
所以△OMN的面积为${S_{△OMN}}=\frac{1}{2}×d×|{MN}|=\sqrt{\frac{{6{m^2}(3{k^2}-{m^2}+2)}}{{{{(3{k^2}+2)}^2}}}}$…①.
因为OM∥PA,ON∥PB,直线OM,ON的斜率乘积为$-\frac{2}{3}$,所以$\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=-\frac{2}{3}$.
所以$\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{(k{x_1}+m)(k{x_2}+m)}}{{{x_1}{x_2}}}=\frac{{{k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}}}{{{x_1}{x_2}}}$=$\frac{{2{m^2}-6{k^2}}}{{3{m^2}-6}}$.
由$\frac{{2{m^2}-6{k^2}}}{{3{m^2}-6}}=-\frac{2}{3}$,得3k2+2=2m2…②
由①②,得${S_{△OMN}}=\sqrt{\frac{{6{m^2}(3{k^2}-{m^2}+2)}}{{{{(3{k^2}+2)}^2}}}}=\sqrt{\frac{{6{m^2}(2{m^2}-{m^2})}}{{4{m^4}}}}=\frac{{\sqrt{6}}}{2}$.
综上所述,${S_{△OMN}}=\frac{{\sqrt{6}}}{2}$. …(13分)
点评 本题考查了直线的斜率公式,三角形的面积公式,注意联立直线方程和椭圆方程,运用韦达定理和弦长公式,考查运算能力,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
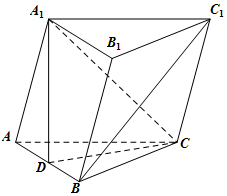 如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
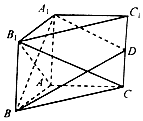 如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.
如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>0 | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ab<b2 | D. | a3-b3<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 矩形 | B. | 梯形 | C. | 正方形 | D. | 菱形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com