
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.
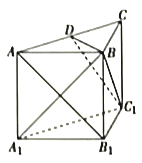
(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见证明;(2)3
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,利用中位线定理证明
,利用中位线定理证明![]() 平面
平面![]() 。
。
(2)通过平移,表示出异面直线![]() 和
和![]() 所成角,结合正弦定理及三角形面积公式求得
所成角,结合正弦定理及三角形面积公式求得![]() 。所以
。所以![]() 可得解。
可得解。
解法一:
(1)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() .
.
在直三棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
所以![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为![]() ,
,![]() 为锐角,
为锐角,
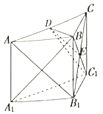
所以![]() 为异面直线
为异面直线![]() 和
和![]() 所成的角,
所成的角,
所以由条件知![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
所以![]() .
.
解法二:(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,
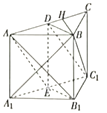
在直三棱柱![]() 中,
中,
四边形![]() 为平行四边形,又
为平行四边形,又![]() 是
是![]() 的中点,
的中点,
所以![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 于
于![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,
,![]() 为锐角,
为锐角,
所以![]() 为异面直线
为异面直线![]() 和
和![]() 所成的角,
所成的角,
所以由条件知![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
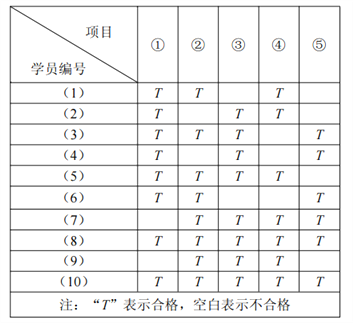
【题目】某市小型机动车驾照“科二”考试中共有5项考查项目,分别记作①,②,③,④,⑤.
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并计算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3(![]() )项的概率.
)项的概率.
(2)“科二”考试中,学员需缴纳150元的报名费,并进行1轮测试(按①,②,③,④,⑤的顺序进行);如果某项目不合格,可免费再进行1轮补测;若第1轮补测中仍有不合格的项目,可选择“是否补考”;若补考则需缴纳300元补考费,并获得最多2轮补测机会,否则考试结束;每1轮补测都按①,②,③,④,⑤的顺序进行,学员在任何1轮测试或补测中5个项目均合格,方可通过“科二”考试,每人最多只能补考1次,某学院每轮测试或补考通过①,②,③,④,⑤各项测试的概率依次为![]() ,且他遇到“是否补考”的决断时会选择补考.
,且他遇到“是否补考”的决断时会选择补考.
①求该学员能通过“科二”考试的概率;
②求该学员缴纳的考试费用![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 周期为
周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数,且
是奇函数,且![]() =10
=10
(1)求![]() 的解析式;
的解析式;
(2)判断函数![]() 在
在![]() 上的单调性,并加以证明.
上的单调性,并加以证明.
(3)函数![]() 在[-3,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
在[-3,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在用二次法求方程3x+3x-8=0在(1,2)内近似根的过程中,已经得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
C.命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题是真命题
有实根”的逆命题是真命题
D.命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() 或
或![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com