
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
【答案】![]()
![]() (或2)
(或2)
【解析】
由已知得△PAC为正三角形,取PC的中点G,得AG⊥PC,且AG![]() .然后证明AG⊥EF,且求得AG与EF的长度,可得截面四边形的面积;再求出四棱锥P﹣AEGF的体积与原正四棱锥的体积,则平面α将此正四棱锥分成的两部分体积的比值可求.
.然后证明AG⊥EF,且求得AG与EF的长度,可得截面四边形的面积;再求出四棱锥P﹣AEGF的体积与原正四棱锥的体积,则平面α将此正四棱锥分成的两部分体积的比值可求.
解:如图,
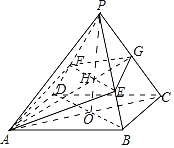
在正四棱锥P﹣ABCD中,由底面边长为2,侧棱长为![]() ,
,
可得△PAC为正三角形,取PC的中点G,得AG⊥PC,且AG![]() .
.
设过AG与PC垂直的平面交PB于E,交PD于F,连接EF,
则EG⊥PC,FG⊥PC,可得Rt△PGE≌Rt△PGF,得GE=GF,PE=PF,
在△PAE与△PAF中,由PA=PA,PE=PF,∠APE=∠APF,得AE=AF.
∴AG⊥EF.
在等腰三角形PBC中,由PB=PC=2![]() ,BC=2,得cos∠BPC
,BC=2,得cos∠BPC![]() ,
,
则在Rt△PGE中,得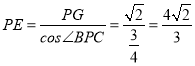 .
.
同理PF![]() ,则EF∥DB,得到
,则EF∥DB,得到![]() .
.
∴![]() ;
;
则![]() .
.
又![]() ,
,
∴平面α将此正四棱锥分成的上下两部分体积的比为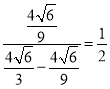 .
.
故答案为:![]() ;
;![]() (或2).
(或2).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的侧棱和底面边长相等,在这个正四棱锥的
的侧棱和底面边长相等,在这个正四棱锥的![]() 条棱中任取两条,按下列方式定义随机变量
条棱中任取两条,按下列方式定义随机变量![]() 的值:
的值:
若这两条棱所在的直线相交,则![]() 的值是这两条棱所在直线的夹角大小(弧度制);
的值是这两条棱所在直线的夹角大小(弧度制);
若这两条棱所在的直线平行,则![]() ;
;
若这两条棱所在的直线异面,则![]() 的值是这两条棱所在直线所成角的大小(弧度制).
的值是这两条棱所在直线所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
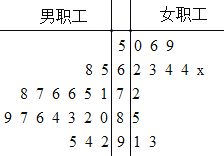
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,....599,600从中抽取60个样本,现提供随机数表的第4行到第6行:
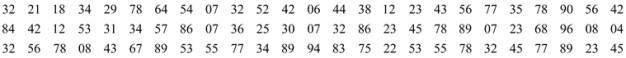
若从表中第6行第6列开始向右依次读取3个数据,则得到的第7个样本编号( )
A.522B.324C.535D.578
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com