
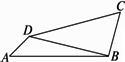
如图,在四边形ABCD中,BC=m,DC=2m,四个内角A、B、C、D之比为3∶7∶4∶10,试求四边形ABCD的面积.
|
解:由题意知,设四个内角A,B,C,D的大小依次为3x,7x,4x,10x,则3x+7x+4x+10x=360°.得x=15°,即A=45°,B=105°,C=60°,D=150°,在△BCD中,由余弦定理,得 BD2=BC2+DC2-2BC·DC·cosC=m2+(2m)2-2×m×2m×cos60°=3m2, ∴BD= ∴S△BCD= 在△BCD中,BD2+BC2=DC2,∴∠DBC=90°.∴∠BDC=30°. 在△BAD中,由正弦定理,得 AB= 又∠ABD=105°-90°=15°, ∴S△ABD= ∴S四边形ABCD=S△ABD+S△BCD= |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
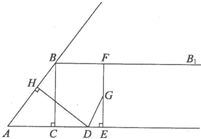 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.| 3 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
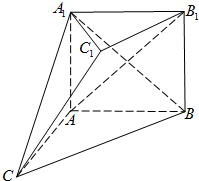 (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com