
【题目】已知函数![]() ,其中函数
,其中函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)确定![]() 与
与![]() 的关系;
的关系;
(2)若![]() ,试讨论函数
,试讨论函数![]() 的单调性.
的单调性.
【答案】(1)![]() ,(2)当
,(2)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
【解析】
试题分析:(1)依题意得![]() ,
,
则![]() .
.
由函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴得:
轴得:![]() ,∴
,∴![]() .
.
(2)由(1)得![]() .
.
∵函数![]() 的定义域为
的定义域为![]() ,
,
∴当![]() 时,
时,![]() .
.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
若![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
由![]() ,得
,得![]() ;
;
若![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
由![]() ,得
,得![]() .
.
若![]() ,即
,即![]() ,在
,在![]() 上恒有
上恒有![]() .
.
综上可得:当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.


科目:高中数学 来源: 题型:
【题目】现有甲、乙两个项目,对甲项目每投资10万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为![]() ;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
(1)求X1,X2的概率分布和均值E(X1),E(X2);
(2)当E(X1)<E(X2)时,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 是一个历史文物展览厅的俯视图,点
是一个历史文物展览厅的俯视图,点![]() 在
在![]() 上,在梯形
上,在梯形![]() 区域内部展示文物,
区域内部展示文物,![]() 是玻璃幕墙,游客只能在
是玻璃幕墙,游客只能在![]() 区域内参观.在
区域内参观.在![]() 上点
上点![]() 处安装一可旋转的监控摄像头.
处安装一可旋转的监控摄像头.![]() 为监控角,其中
为监控角,其中![]() 、
、![]() 在线段
在线段![]() (含端点)上,且点
(含端点)上,且点![]() 在点
在点![]() 的右下方.经测量得知:
的右下方.经测量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() 的面积为
的面积为![]() 平方米.
平方米.

(1)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线C: ![]() ﹣y2=1(a>0)的右焦点为F,点A,B分别在C的两条渐近线AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).
﹣y2=1(a>0)的右焦点为F,点A,B分别在C的两条渐近线AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点). 
(1)求双曲线C的方程;
(2)过C上一点P(x0 , y0)(y0≠0)的直线l: ![]() ﹣y0y=1与直线AF相交于点M,与直线x=
﹣y0y=1与直线AF相交于点M,与直线x= ![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时, ![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有株树木的底部周长小于100cm. 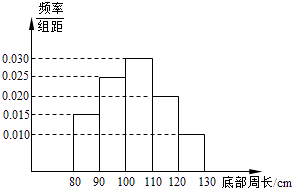
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO= ![]() .
. 
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x1 , x2 , x3 , 随机变量X表示x1 , x2 , x3中的最大数,求X的概率分布和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在政府的帮扶下,准备转型生产一种特殊机器,生产需要投入固定成本![]() 万元,生产与销售均已百台计数,且每生产
万元,生产与销售均已百台计数,且每生产![]() 台,还需增加可变成本
台,还需增加可变成本![]() 万元,若市场对该产品的年需求量为
万元,若市场对该产品的年需求量为![]() 台,每生产
台,每生产![]() 百台的实际销售收入近似满足函数
百台的实际销售收入近似满足函数![]() .
.
(![]() )试写出第一年的销售利润
)试写出第一年的销售利润![]() (万元)关于年产量
(万元)关于年产量![]() (单位:百台,
(单位:百台,![]() ,
,![]() )的函数关系式:(说明:销售利润=实际销售收入-成本)
)的函数关系式:(说明:销售利润=实际销售收入-成本)
(![]() )因技术等原因,第一年的年生产量不能超过
)因技术等原因,第一年的年生产量不能超过![]() 台,若第一年的年支出费用
台,若第一年的年支出费用![]() (万元)与年产量
(万元)与年产量![]() (百台)的关系满足
(百台)的关系满足![]() ,问年产量
,问年产量![]() 为多少百台时,工厂所得纯利润最大?
为多少百台时,工厂所得纯利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com