
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示. 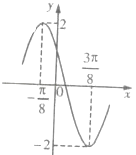
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)求函数f(x)在[﹣ ![]() ,
, ![]() ]上的单调减区间.
]上的单调减区间.
【答案】
(1)解:由题意知: ![]() ,∴
,∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() (k∈Z),
(k∈Z), ![]() (k∈Z),又|φ|<π,∴
(k∈Z),又|φ|<π,∴ ![]() .
.
∴函数f(x)的解析式: ![]()
(2)解:由 ![]() ,k∈Z,得
,k∈Z,得 ![]() ,
,
所以f(x)的增区间为 ![]() ,k∈Z
,k∈Z
(3)解:再根据x∈[﹣ ![]() ,
, ![]() ],可得函数f(x)在[﹣
],可得函数f(x)在[﹣ ![]() ,
, ![]() ]上的单调减区间为[﹣
]上的单调减区间为[﹣ ![]() ,
, ![]() ].
].
【解析】(1)由图象相邻的最高点和最低点的横坐标之差可求最小正周期,最高点纵坐标可求得振幅,将最高点代入解析式中求初相,可得函数的解析式(2)正弦函数的单调增区间为 ![]() ,所以可令
,所以可令 ![]() ,由此解出x的范围,即为要求的f(x)的单调增区间.(3)由(2)结合x∈[﹣
,由此解出x的范围,即为要求的f(x)的单调增区间.(3)由(2)结合x∈[﹣ ![]() ,
, ![]() ],可得函数f(x)在[﹣
],可得函数f(x)在[﹣ ![]() ,
, ![]() ]上的单调减区间.
]上的单调减区间.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
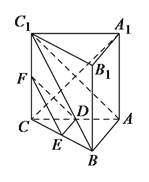
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若线段![]() 上的点
上的点![]() 满足平面
满足平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并说明理由.
的位置,并说明理由.
(Ⅲ)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为圆
,左、右焦点分别为圆![]() ,
, ![]() 是
是![]() 上一点,
上一点, ![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() 时,线段
时,线段![]() 上取点
上取点![]() ,且
,且![]() 满足
满足![]() ,证明点
,证明点![]() 总在某定直线上,并求出该定直线.
总在某定直线上,并求出该定直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B 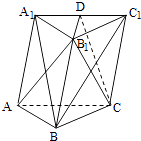
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com