
分析 (1)由f(x)的对称轴方程以及图象过点(1,13),求出b、c的值,从而写出f(x)的解析式;
(2)化函数g(x)为分段函数,画出函数的图象,结合图象,求出g(x)在区间[t,2]上的最小值H(t);
(3)设函数P(m,n2),m∈N*,n∈N*,可定m2+m+11=n2,即可得出结论.
解答 解:(1)∵二次函数f(x)=x2+bx+c的对称轴方程为$x=-\frac{1}{2}$,
∴b=1.…(2分)
又∵二次函数f(x)=x2+bx+c的图象过点(1,13),
∴1+b+c=13,
∴c=11,
∴f(x)=x2+x+11…(4分)
(2)由(1)得$g(x)=({x-2})•|x|=\left\{\begin{array}{l}{({x-1})^2}-1,({x≥0})\\-{({x-1})^2}+1,({x<0})\end{array}\right.$.…(6分)
画出函数图象,如图: ;
;
结合图象可知当1≤t<2时,$g{(x)_{min}}={t^2}-2t$;…(7分)
当$1-\sqrt{2}≤t<1$时,g(x)min=-1;…(8分)
当$t<1-\sqrt{2}$时,$g{(x)_{min}}=-{t^2}+2t$.…(9分)
综上所述$H(t)=\left\{\begin{array}{l}-{t^2}-2t,1≤t<2\\-1,1-\sqrt{2}≤t<1\\-{t^2}+2t,t<1-\sqrt{2}\end{array}\right.$.…(10分)
(3)如果函数y=f(x)的图象上存在符合要求的点,
设函数P(m,n2),m∈N*,n∈N*,∴m2+m+11=n2.…(11分)
∵m(m+1)=n2-11>0,
∴由m(m+1)为偶数,有n为奇数,且n≥4,
∴n=5,7,9,11.
验证∴n=11,m=10,
∴存在点(10,121)…(14分)
点评 本题考查了求函数的解析式以及求函数在某一区间上的最值情况,解题时应结合函数的图象与性质来解答,是易错题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
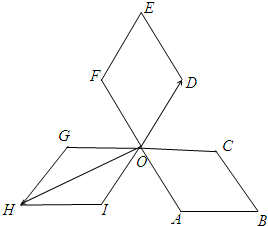 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 5 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com