【题目】
不是直角三角形，它的三个角
所对的边分别为
，已知
.
（1）求证： 
；
（2）如果
，求
面积的最大值.
【答案】（1）见解析；（2）48
【解析】试题分析：（1）由
，根据正弦定理及两角和的正弦公式化简可得
，因为
不是直角三角形，所以
，由正弦定理可得
；（2）视
为定点,求出满足
条件下
的轨迹为一个圆，圆心在直
上，当
上升到离直线
最远时面积最大.
试题解析：（1）由
，根据正弦定理可得
， 
，因为
不是直角三角形，所以
，由正弦定理可得
；
（2）方法一：b=2a.c=12，余弦定理用a表示cosC,表示出sinC,进而用a表示出
,求出该函数的最大值.(最费力的做法)
方法二:视A.B为定点,求出满足b=2a条件下C的轨迹为一个圆，圆心在直线AB上，当C上升到离直线AB最远时面积最大。
方法三：利用海伦公式直接将面积表示为a的函数
方法三为最简捷办法，凡只涉及边的面积问题可优先想到海伦公式。
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为
（
为参数，
），以原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）写出曲线的普通方程和曲线的直角坐标方程；
（2）已知点
是曲线上一点，若点到曲线的最小距离为
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图如图所示．以组距为5将数据分组成[0，5)，[5，10)，…，[30，35)，[35，40]时，所作的频率分布直方图是( )
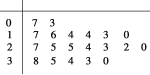
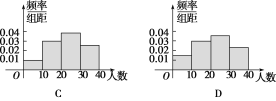
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)＝a2x2(a＞0)，g(x)＝bln x.
（1）若函数y＝f(x)图象上的点到直线x－y－3＝0距离的最小值为2
，求a的值；
（2）对于函数f(x)与g(x)定义域上的任意实数x，若存在常数k，m，使得f(x)≥kx＋m和g(x)≤kx＋m都成立，则称直线y＝kx＋m为函数f(x)与g(x)的“分界线”．设a＝
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标
中，圆
，圆
。
(Ⅰ)在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆
的极坐标方程，并求出圆
的交点坐标(用极坐标表示)；
(Ⅱ)求圆
的公共弦的参数方程。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以A表示值域为R的函数组成的集合，B表示具有如下性质的函数
组成的集合：对于函数
，存在一个正数M，使得函数
的值域包含于区间[-M，M]。例如，当
， 
时， 
，现有如下命题：
①设函数
的定义域为D，则“
”的充要条件是“
”；
②若函数
，则
有最大值和最小值；
③若函数
， 
的定义域相同，且
， 
，则
④若函数
，则
有最大值且
，
其中的真命题有_____________。（写出所有真命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为减少汽车尾气排放,提高空气质量,各地纷纷推出汽车尾号限行措施.为做好此项工作，某市交警支队对市区各交通枢纽进行调查统计，表中列出了某交通路口单位时间内通过的1000辆汽车的车牌尾号记录：
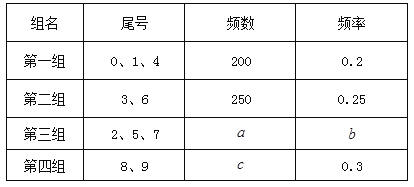
由于某些数据缺失，表中以英文字母作标识.请根据图表提供的信息计算：
（Ⅰ）若采用分层抽样的方法从这1000辆汽车中抽出20辆，了解驾驶员对尾号限行的建议，应分别从一、二、三、四组中各抽取多少辆？
（Ⅱ）以频率代替概率，在此路口随机抽取4辆汽车，奖励汽车用品.用
表示车尾号在第二组的汽车数目，求
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
