
【题目】给出以下四个结论:
(1)若函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域是
的定义域是![]() ;
;
(2)函数![]() (其中
(其中![]() ,且
,且![]() )的图象过定点
)的图象过定点![]() ;
;
(3)当![]() 时,幂函数
时,幂函数![]() 的图象是一条直线;
的图象是一条直线;
(4)若![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.
其中所有正确结论的序号是_________.
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆C的方程;
(2)已知两条互相垂直的直线![]() ,
,![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 四点,求四边形
四点,求四边形![]() 面积的的取值范围.
面积的的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司2001年至2017年新产品研发费用![]() (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量![]() 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①:![]() ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量![]() 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②:![]() .
.

(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
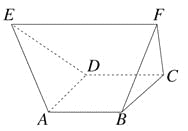
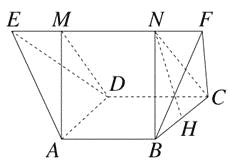
【题目】如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过坐标原点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
①是否存在常数![]() ,满足
,满足![]() ?若存在,求出这个常数;若不存在,请说明理由;
?若存在,求出这个常数;若不存在,请说明理由;
②若![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com