
【题目】已知数列![]() 的首项
的首项![]() ,其前n项和为
,其前n项和为![]() ,对于任意正整数
,对于任意正整数![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() .
.
①若![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
②若数列![]() 都是等比数列,求证:数列
都是等比数列,求证:数列![]() 中至多存在三项.
中至多存在三项.
【答案】(1)![]() (2)①见证明;②见证明;
(2)①见证明;②见证明;
【解析】
(1)由![]() 可得
可得![]() ,进而得到数列
,进而得到数列![]() 的通项公式;
的通项公式;
(2)①由![]() 可得
可得![]() ,利用待定系数法可得
,利用待定系数法可得![]() 从而得证;②利用反证法证明即可.
从而得证;②利用反证法证明即可.
(1)令![]() ,则由
,则由![]() ,得
,得![]()
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,且当n=1时,此式也成立.
,且当n=1时,此式也成立.
所以数列![]() 的通项公式为
的通项公式为![]()
(2)①【证法一】因为![]() ,
,
![]() ,
,
所以![]() .
.
由![]() 得
得![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以数列![]() 是等差数列.
是等差数列.
【证法二】
因为![]()
所以![]()
所以![]() .
.
所以![]() ,
,
所以![]() ,
,
记![]()
![]() ,
,
两式相减得![]() ,
,
所以![]() ,
,
所以,当![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,
,
所以,当![]() 时,
时,![]() ,当n=1时,上式也成立,
,当n=1时,上式也成立,
所以![]() ,(iii)
,(iii)
所以数列![]() 是等差数列.
是等差数列.
【证法三】
因为![]()
所以![]() ,(i)
,(i)
所以![]() ,(ii)
,(ii)
(i)-(ii)得![]() ,(iii)
,(iii)
所以![]() ,(iv)
,(iv)
(iii)-(iv)得![]() ,
,
所以![]() .
.
由![]() 知
知![]() .
.
所以![]() ,
,
所以数列![]() 是等差数列
是等差数列
②不妨设数列![]() 超过三项,令
超过三项,令![]() ,
,
由题意![]() ,则有
,则有![]() ,
,
即![]() ,
,
代入![]() ,整理得
,整理得![]() (*),
(*),
若p=q=1,则![]() ,与条件矛盾;
,与条件矛盾;
若![]() ,当n=1时,
,当n=1时,![]() ,①
,①
当n=2时,![]() ,②
,②
②÷①得,p=q,代入(*)得b=c,所以![]() ,与条件矛盾.
,与条件矛盾.
故这样的数列![]() 至多存在三项.
至多存在三项.


科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为A,上顶点为B,若
,右顶点为A,上顶点为B,若![]() ,
,![]() ,
,![]() 成等比数列,椭圆C上的点到焦点
成等比数列,椭圆C上的点到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 过该椭圆的右焦点
过该椭圆的右焦点![]() 作倾角为
作倾角为![]() 的直线与椭圆交于M,N两点,求
的直线与椭圆交于M,N两点,求![]() 的内切圆的半径.
的内切圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为:
的方程为:![]()
![]() 当极点
当极点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求直线
时,求直线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若直线
若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的55名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | |
男生 | 20 | 5 |
女生 | 10 | 20 |
临界值参考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: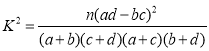 ,其中
,其中![]() )
)
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过![]() 的前提下,认为“喜欢“应用统计”课程与性别有关”
的前提下,认为“喜欢“应用统计”课程与性别有关”
B.在犯错误的概率不超过![]() 的前提下,认为“喜欢“应用统计”课程与性别无关”
的前提下,认为“喜欢“应用统计”课程与性别无关”
C.有![]() 以上的把握认为“喜欢应用统计”课程与性别有关”
以上的把握认为“喜欢应用统计”课程与性别有关”
D.有![]() 以上的把握认为“喜欢“应用统计”课程与性别无关”
以上的把握认为“喜欢“应用统计”课程与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系![]() 中,已知正四棱锥
中,已知正四棱锥![]() 的高
的高![]() ,点
,点![]() 和
和![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,且
轴上,且![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
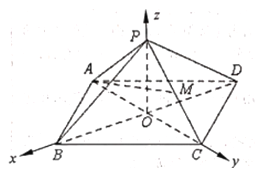
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com